
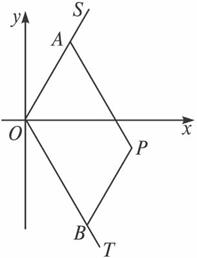
(1)求m·n的值;
(2)求点P的轨迹C的方程,并说明它表示怎样的曲线;
(3)若直线l过点E(2,0)交(2)中曲线C于M、N两点(M、N、E三点互不相同),且![]() ,求l的方程.
,求l的方程.
(文)已知等比数列{an},Sn是其前n项的和,且a1+a3=5,S4=15.
(1)求数列{an}的通项公式;
(2)设bn=![]() +log2an,求数列{bn}的前n项和Tn;
+log2an,求数列{bn}的前n项和Tn;
(3)比较(2)中Tn与![]() n3+2(n=1,2,3,…)的大小,并说明理由.
n3+2(n=1,2,3,…)的大小,并说明理由.
答案:(理)解:(1)由已知,得![]() =(m,
=(m,![]() m)·(n,
m)·(n,![]() n)=-2mn=-
n)=-2mn=-![]() .
.
∴m·n=![]() .
.
(2)设P点坐标为(x,y)(x>0),由![]() ,得
,得
(x,y)=(m,![]() m)+(n,
m)+(n,![]() n)=(m+n,
n)=(m+n,![]() (m-n)).
(m-n)).
∴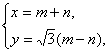 消去m,n,可得x2
消去m,n,可得x2![]() =4mn,又因mn=
=4mn,又因mn=![]() ,
,
∴P点的轨迹方程为x2![]() =1(x>0).
=1(x>0).
它表示以坐标原点为中心,焦点在x轴上,且实轴长为2,焦距为4的双曲线x2![]() =1的右支.
=1的右支.
(3)设直线l的方程为x=ty+2,将其代入C的方程,得3(ty+2)2-y2=3,即(3t2-1)y2+12ty+9=0.
易知(3t2-1)≠0(否则,直线l的斜率为±3,它与渐近线平行,不符合题意).
又Δ=144t2-36(3t2-1)=36(t2+1)>0,设M(x1,y1),N(x2,y2),则y1+y2=![]() ,y1y2=
,y1y2=![]() .
.
∵l与C的两个交点M、N在y轴右侧,x1x2=(ty1+2)(ty2+2)=t2y1y2+2t(y1+y2)+4
=t2·![]() +2t·
+2t·![]() +4=
+4=![]() .∴3t2-1<0.又∵t=0不合题意,∴0<t2<
.∴3t2-1<0.又∵t=0不合题意,∴0<t2<![]() .
.
又由x1+x2>0,同理,可得0<t2<![]() .
.
由![]() ,得(2-x1,-y1)=3(x2-2,y2),∴
,得(2-x1,-y1)=3(x2-2,y2),∴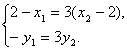
由y1+y2=-3y2+y2=-2y2=![]() ,得y2=
,得y2=![]() .由y1y2=(-3y2)y2=-3y22=
.由y1y2=(-3y2)y2=-3y22=![]() ,
,
得y22=![]() .消去y2,得
.消去y2,得![]() =
=![]() .解之,得t2=
.解之,得t2=![]() ,满足0<t2<
,满足0<t2<![]() ,
,
故所求直线l存在,其方程为![]() x-y-2
x-y-2![]() =0或
=0或![]() x+y-2
x+y-2![]() =0.
=0.
(文)解:(1)设数列{an}的公比为q,则
方法一:a1+a3=a1+a1q2=a1(1+q2)=5,S4-(a1+a3)=a2+a4=a1q(1+q2)=10,
∴q=2,a1=1,则an=2n-1.
方法二:易知q≠1,则a1+a3=a1+a1q2=a1(1+q2)=5,
S4=![]() =a1(1+q)(1+q2)=15,则1+q=3.
=a1(1+q)(1+q2)=15,则1+q=3.
(以下同方法一)
(2)由(1)可得,bn=![]() +log22n-1=
+log22n-1=![]() +(n-1)=n+
+(n-1)=n+![]() ,
,
所以数列{bn}是一个以![]() 为首项,1为公差的等差数列.
为首项,1为公差的等差数列.
∴Tn=![]()
= .
.
(3)∵(![]() n3+2)-Tn=
n3+2)-Tn=![]() (n3-n2-4n+4)=
(n3-n2-4n+4)=![]() (n-1)(n-2)(n+2),
(n-1)(n-2)(n+2),
∴当n=1、2时,![]() (n-1)(n-2)(n+2)=0,即Tn=
(n-1)(n-2)(n+2)=0,即Tn=![]() n3+2.
n3+2.
当n≥3时,![]() (n-1)(n-2)(n+2)>0,即Tn<
(n-1)(n-2)(n+2)>0,即Tn<![]() n3+2.
n3+2.
综上可知,n=1、2时,Tn=![]() n3+2;n≥3时,Tn<
n3+2;n≥3时,Tn<![]() n3+2.
n3+2.


科目:高中数学 来源: 题型:
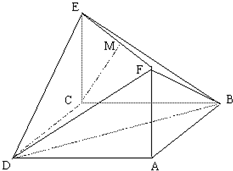 (理)如图,已知矩形ACEF的边CE与正方形ABCD所在平面垂直,AB=
(理)如图,已知矩形ACEF的边CE与正方形ABCD所在平面垂直,AB=| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (理)如图,P为△ABC所在平面外一点,且PA⊥平面ABC,∠ACB=90°,过点A作垂直于PC的截面ADE,截面交PC于点D,交PB于点E.
(理)如图,P为△ABC所在平面外一点,且PA⊥平面ABC,∠ACB=90°,过点A作垂直于PC的截面ADE,截面交PC于点D,交PB于点E.查看答案和解析>>
科目:高中数学 来源: 题型:

| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
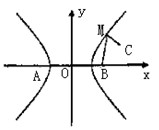
(08年福州质检理)如图,M是以A、B为焦点的双曲线![]() 右支上任一点,若点M到点C(3,1)与点B的距离之和为S,则S的取值范围是 ( )
右支上任一点,若点M到点C(3,1)与点B的距离之和为S,则S的取值范围是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com