
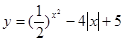 的一个单调减区间为_______.
的一个单调减区间为_______. 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:高中数学 来源:不详 题型:解答题
 其中
其中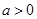 .(1)求函数
.(1)求函数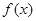 的单调区间;(2)若函数
的单调区间;(2)若函数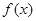 在区间
在区间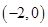 内恰有两个零点,求
内恰有两个零点,求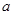 的取值范围;
的取值范围; 时,设函数
时,设函数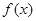 在区间
在区间 上的最大值为
上的最大值为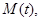 最小值为
最小值为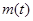 ,记
,记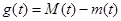 ,求函数
,求函数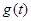 在区间
在区间 上的最小值.
上的最小值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
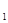 与该车间的工人人数x成反比,而生产配件B成本费y
与该车间的工人人数x成反比,而生产配件B成本费y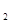 与该车间的工人人数x成正比,如果该车间的工人人数为10人时,这两项费用y
与该车间的工人人数x成正比,如果该车间的工人人数为10人时,这两项费用y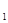 和y
和y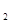 分别为2万元和8万元,那么要使这两项费用之和最小,该车间的工人人数x应为多少?
分别为2万元和8万元,那么要使这两项费用之和最小,该车间的工人人数x应为多少?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com