
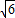 -2)R
-2)R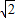 -1)R
-1)R R
R R
R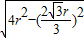 =
=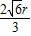
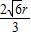 -x)2+(
-x)2+(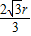 )2
)2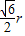
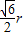 +r,
+r,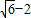 )R.
)R.

科目:高中数学 来源:数学教研室 题型:044
在棱长2R的正方体容器内装满水,先把半径为R的球放入水,然后再放入一个小球,使它们淹没在水中,当小球的半径为多大时,使溢出的水量最大?此时投放这两个球时溢出的水约占正方体的体积的百分之几?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com