
[2012·课标全国卷] 如图1-4,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC=![]() AA1,D是棱AA1的中点.
AA1,D是棱AA1的中点.
(1)证明:平面BDC1⊥平面BDC;
(2)平面BDC1分此棱柱为两部分,求这两部分体积的比.
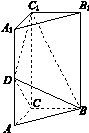
图1-4
 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案科目:高中数学 来源: 题型:
[2012·课标全国卷] 如图1-2,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为( )

图1-3
A.6 B.9 C.12 D.18
查看答案和解析>>
科目:高中数学 来源: 题型:
[2012·课标全国卷] 如图1-4,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC=![]() AA1,D是棱AA1的中点.
AA1,D是棱AA1的中点.
(1)证明:平面BDC1⊥平面BDC;
(2)平面BDC1分此棱柱为两部分,求这两部分体积的比.
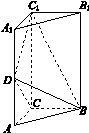
图1-4
查看答案和解析>>
科目:高中数学 来源: 题型:
(2012年高考新课标全国卷理科20)(本小题满分12分)
设抛物线![]() 的焦点为
的焦点为![]() ,准线为
,准线为![]() ,
,![]() ,已知以
,已知以![]() 为圆心,
为圆心,
![]() 为半径的圆
为半径的圆![]() 交
交![]() 于
于![]() 两点;
两点;
(1)若![]() ,
,![]() 的面积为
的面积为![]() ;求
;求![]() 的值及圆
的值及圆![]() 的方程;
的方程;
(2)若![]() 三点在同一直线
三点在同一直线![]() 上,直线
上,直线![]() 与
与![]() 平行,且
平行,且![]() 与
与![]() 只有一个公共点,
只有一个公共点,
求坐标原点到![]() 距离的比值.
距离的比值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com