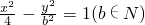练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    双曲线数学公式的两个焦点为F1、F2，P为双曲线上一点，|OP|＜5，|PF1|、|F1F2|、|PF2|成等比数列，则b2=________．

    1
    分析：通过等比数列双曲线的定义，余弦定理推出：|OP|2=20+3b2．利用|OP|＜5，b∈N，求出b的值．
    解答：由题意，|PF1|、|F1F2|、|PF2|成等比数列可知，|F1F2|2=|PF1||PF2|，
    即4c2=|PF1||PF2|，
    由双曲线的定义可知|PF1|-|PF2|=4，即|PF1|2+|PF2|2-2|PF1||PF2|=16，
    可得|PF1|2+|PF2|2-8c2=16…①
    设∠POF1=θ，则∠POF2=π-θ，
    由余弦定理可得：|PF2|2=c2+|OP|2-2|OF2||OP|cos（π-θ），|PF1|2=c2+|OP|2-2|OF1||OP|cosθ，
    |PF2|2+PF1|2=2c2+2|OP|2，…②，
    由①②化简得：|OP|2=8+3c2=20+3b2．
    因为|OP|＜5，b∈N，所以20+3b2＜25．
    所以b=1．
    故答案为：1．
    点评：本题考查双曲线的定义，余弦定理以及等比数列的应用，是有难度的综合问题，考查分析问题解决问题的能力．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知双曲线C：
    x2
    a2
    -
    y2
    b2
    -1(a＞0，b＞0)    的两个焦点为F：(-2，0)，F：(2，0)，点P(3，
    		7
    )
    的曲线C上．
    （Ⅰ）求双曲线C的方程；
    （Ⅱ）记O为坐标原点，过点Q（0，2）的直线l与双曲线C相交于不同的两点E、F，若△OEF的面积为2
    		2
    ，求直线l的方程．

    查看答案和解析>>

    科目：高中数学 来源：2009年高考数学第二轮复习热点专题测试卷：平面解析几何(含详解) 题型：044

    已知双曲线的两个焦点为F：(－2，0)，F：(2，0)，点P(3，)的曲线C上．

    (Ⅰ)求双曲线C的方程；

    (Ⅱ)记O为坐标原点，过点Q(0，2)的直线l与双曲线C相交于不同的两点E、F，若△OEF的面积为求直线l的方程

    查看答案和解析>>

    科目：高中数学 来源：2009年高考数学第二轮执点专题测试、平面解析几何(含详解) 题型：044

    已知双曲线的两个焦点为F：(－2，0)，F：(2，0)，点P(3，)的曲线C上．

    (Ⅰ)求双曲线C的方程；

    (Ⅱ)记O为坐标原点，过点Q(0，2)的直线l与双曲线C相交于不同的两点E、F，若△OEF的面积为求直线l的方程

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    双曲线的两个焦点为F­1，F­2 ，点P在双曲线上，△的面积为，则                              

    A．2　　                     B．                        C．－2　　                 D．  

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    双曲线的两个焦点为F­1，F­2 ，点P在双曲线上，的面积为，则                     

    A．2　　                 B．　              C．－2　　             D．－

    查看答案和解析>>

    同步练习册答案