
分析 (1)令y=x可得f(x)=$\frac{1}{2}$+$\frac{1}{2}$f(2x);
(2)根据数学归纳法的证明步骤,即可证明结论.
解答 证明:(1)令y=x可得f(2x)+1=f(x)+f(x),
所以f(x)=$\frac{1}{2}$+$\frac{1}{2}$f(2x)…(3分)
(2)①当n=1时,x∈[$\frac{1}{4}$,$\frac{1}{2}$],则2x∈[$\frac{1}{2}$,1],所以f(2x)≤0
又f(2x)+1=2f(x),所以f(x)=$\frac{1}{2}$+$\frac{1}{2}$f(2x)≤$\frac{1}{2}$=1-$\frac{1}{2}$
所以当n=1时命题成立.…(7分)
②假设n=k时命题成立,即当x∈[$\frac{1}{{2}^{k+1}}$,$\frac{1}{{2}^{k}}$](k∈N*)时,f(x)≤1-$\frac{1}{{2}^{k}}$
则当n=k+1时,x∈[$\frac{1}{{2}^{k+2}}$,$\frac{1}{{2}^{k+1}}$],2x∈[$\frac{1}{{2}^{k+1}}$,$\frac{1}{{2}^{k}}$],则
f(x)=$\frac{1}{2}$+$\frac{1}{2}$f(2x)≤$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{{2}^{k+1}}$=1-$\frac{1}{{2}^{k+1}}$
当n=k+1时命题成立.…(15分)
综上①②可知,当x∈[$\frac{1}{{2}^{n+1}}$,$\frac{1}{{2}^{n}}$](n∈N*)时,f(x)≤1-$\frac{1}{{2}^{n}}$.…(16分)
点评 本题主要考查数学归纳法,数学归纳法的基本形式:设P(n)是关于自然数n的命题,若1°P(n0)成立(奠基),2°假设P(k)成立(k≥n0),可以推出P(k+1)成立(归纳),则P(n)对一切大于等于n0的自然数n都成立.


 高中必刷题系列答案
高中必刷题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
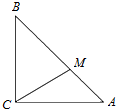 如图,在△ABC中,∠ACB=90°,且AC=BC=3,点M满足$\overrightarrow{BM}=2\overrightarrow{MA}$,
如图,在△ABC中,∠ACB=90°,且AC=BC=3,点M满足$\overrightarrow{BM}=2\overrightarrow{MA}$,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | -$\frac{8}{9}$ | C. | -$\frac{7}{9}$ | D. | $\frac{7}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | 3 | 4 | 5 | 6 | 7 |
| y | 5.8 | 8.2 | 9.7 | 12.2 | 14.1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第9项 | B. | 第8项 | C. | 第9项和第10项 | D. | 第8项和第9项 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
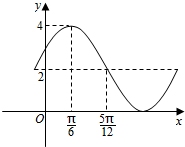 已知函数y=Asin(ωx+φ)+B的一部分图象如图所示,如果A>0,ω>0,|φ|<$\frac{π}{2}$,则其解析式为y=2sin(2x+$\frac{π}{6}$)+2..
已知函数y=Asin(ωx+φ)+B的一部分图象如图所示,如果A>0,ω>0,|φ|<$\frac{π}{2}$,则其解析式为y=2sin(2x+$\frac{π}{6}$)+2..查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com