
【题目】椭圆![]() 的离心率为
的离心率为![]() ,左焦点
,左焦点![]() 到直线
到直线![]() 的距离为10,圆
的距离为10,圆![]() .
.
(1)求椭圆的方程;
(2)若![]() 是椭圆上任意一点,
是椭圆上任意一点,![]() 为圆
为圆![]() 的任一直径,求
的任一直径,求![]() 的取值范围;
的取值范围;
(3)是否存在以椭圆上点![]() 为圆心的圆
为圆心的圆![]() ,使得过圆
,使得过圆![]() 上任意一点
上任意一点![]() 作圆
作圆![]() 的切线,切点为
的切线,切点为![]() ,都满足
,都满足![]() ?若存在,求出圆
?若存在,求出圆![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 右焦点与抛物线
右焦点与抛物线![]() 的焦点重合,以原点为圆心、椭圆短半轴长为半径的圆与直线
的焦点重合,以原点为圆心、椭圆短半轴长为半径的圆与直线![]() 相切.
相切.
(1)求椭圆的方程
(2)若直线![]() 与y轴交点为P,A、B是椭圆上两个动点,它们在y轴两侧,
与y轴交点为P,A、B是椭圆上两个动点,它们在y轴两侧,![]() ,
,![]() 的平分线与y轴重合,则直线AB是否过定点,若过定点,求这个定点坐标,若不过定点说明理由.
的平分线与y轴重合,则直线AB是否过定点,若过定点,求这个定点坐标,若不过定点说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的焦距为2,且过点
的焦距为2,且过点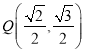 .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
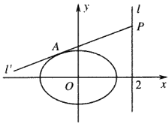
(2)若![]() 为坐标原点,
为坐标原点,![]() 为直线
为直线![]() 上的一动点,过点
上的一动点,过点![]() 作直线
作直线![]() 与椭圆相切于点
与椭圆相切于点![]() ,若
,若![]() 的面积
的面积![]() 为
为![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角梯形ABCD中(如图1),![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,点E在CD上,且
,点E在CD上,且![]() ,将
,将![]() 沿AE折起,使得平面
沿AE折起,使得平面![]() 平面ABCE(如图2),G为AE中点.
平面ABCE(如图2),G为AE中点.

(Ⅰ)求四棱锥![]() 的体积;
的体积;
(Ⅱ)在线段BD上是否存在点P,使得![]() 平面ADE?若存在,求
平面ADE?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,
中,![]() 为坐标原点,
为坐标原点,![]() ,
,![]() ,已知
,已知![]() 是以
是以![]() 为底边,且边
为底边,且边![]() 平行于
平行于![]() 轴的等腰三角形.
轴的等腰三角形.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)已知直线![]() 交
交![]() 轴于点
轴于点![]() ,且与曲线
,且与曲线![]() 相切于点
相切于点![]() ,点
,点![]() 在曲线
在曲线![]() 上,且直线
上,且直线![]() 轴,点
轴,点![]() 关于点
关于点![]() 的对称点为点
的对称点为点![]() ,试判断点
,试判断点![]() 、
、![]() 、
、![]() 三点是否共线,并说明理由.
三点是否共线,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() :
:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,.
,.![]() .,
.,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() …的前n项和为
…的前n项和为![]() ,正整数
,正整数![]() ,
,![]() 满足:①
满足:①![]() ,②
,②![]() 是满足不等式
是满足不等式![]() 的最小正整数,则
的最小正整数,则![]() ( )
( )
A.6182B.6183C.6184D.6185
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为准备参加市运动会,对本校甲、乙两个田径队中![]() 名跳高运动员进行了测试,并用茎叶图表示出本次测试
名跳高运动员进行了测试,并用茎叶图表示出本次测试![]() 人的跳高成绩(单位:
人的跳高成绩(单位:![]() ).跳高成绩在
).跳高成绩在![]() 以上(包括
以上(包括![]() )定义为“合格”,成绩在
)定义为“合格”,成绩在![]() 以下(不包括
以下(不包括![]() )定义为“不合格”.鉴于乙队组队晚,跳高成绩相对较弱,为激励乙队队队,学校决定只有乙队中“合格”者才能参加市运动会开幕式旗林队.
)定义为“不合格”.鉴于乙队组队晚,跳高成绩相对较弱,为激励乙队队队,学校决定只有乙队中“合格”者才能参加市运动会开幕式旗林队.
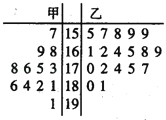
(1)求甲队队员跳高成绩的中位数;
(2)如果用分层抽样的方法从甲、乙两队所有的运动员中共抽取![]() 人,则
人,则![]() 人中“合格”与“不合格”的人数各为多少;
人中“合格”与“不合格”的人数各为多少;
(3)若从所有“合格”运动员中选取![]() 名,用
名,用![]() 表示所选运动员中能参加市运动会开幕式旗林队的人数,试求
表示所选运动员中能参加市运动会开幕式旗林队的人数,试求![]() 的概率.
的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com