
【题目】已知数列![]() :
:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,.
,.![]() .,
.,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() …的前n项和为
…的前n项和为![]() ,正整数
,正整数![]() ,
,![]() 满足:①
满足:①![]() ,②
,②![]() 是满足不等式
是满足不等式![]() 的最小正整数,则
的最小正整数,则![]() ( )
( )
A.6182B.6183C.6184D.6185
【答案】B
【解析】
由题意可知,数列![]() 的规律为:分母为
的规律为:分母为![]() 的项有
的项有![]() 项.将数列
项.将数列![]() 中的项排成杨辉三角数阵且使得第k行每项的分母为
中的项排成杨辉三角数阵且使得第k行每项的分母为![]() ,该行有
,该行有![]() 项,那么
项,那么![]() 位于数阵第11行最后一项,通过计算得
位于数阵第11行最后一项,通过计算得![]() ;设数阵中第k行各项之和为
;设数阵中第k行各项之和为![]() ,则
,则![]() ,故通过计算可得满足
,故通过计算可得满足![]() 的最小正整数
的最小正整数![]() ,即可得出最后结果.
,即可得出最后结果.
由题意可知,数列![]() 的规律为:分母为
的规律为:分母为![]() 的项有
的项有![]() 项.将数列
项.将数列![]() 中的项排成杨辉三角数阵且使得第k行每项的分母为
中的项排成杨辉三角数阵且使得第k行每项的分母为![]() ,该行有
,该行有![]() 项,如下所示:
项,如下所示:
| ||||||
|
|
| ||||
|
|
|
|
|
|
|
对于①,![]() 位于数阵第11行最后一项,对应于数列
位于数阵第11行最后一项,对应于数列![]() 的项数为
的项数为
![]() ,
,
∴![]() ;
;
对于②,数阵中第k行各项之和为![]() ,
,
则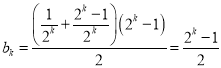 ,
,
且数列![]() 的前k项之和
的前k项之和
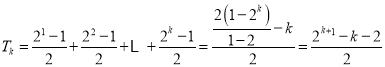 ,
,
![]() ,
,
而![]() ,
,
故恰好满足![]() 的项
的项![]() 位于第11行.
位于第11行.
假设![]() 位于第m项,则有
位于第m项,则有
![]() ,
,
可得出![]() .
.
由于![]() ,
,![]() ,
,
则![]() ,∴
,∴![]() .
.
因为前10行最后一项位于![]() 的第
的第
![]() 项,
项,
因此,满足![]() 的最小正整数
的最小正整数![]() ,
,
所以![]() .
.
故选:B


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为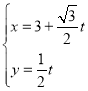 (
(![]() 为参数),在以坐标原点
为参数),在以坐标原点![]() 为极点、以
为极点、以![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,若直线
,若直线![]() 与曲线
与曲线![]() 交于
交于![]() 、
、![]() 两点.
两点.
(1)求线段![]() 的中点
的中点![]() 的直角坐标;
的直角坐标;
(2)设点![]() 是曲线
是曲线![]() 上任意一点,求
上任意一点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 的离心率为
的离心率为![]() ,左焦点
,左焦点![]() 到直线
到直线![]() 的距离为10,圆
的距离为10,圆![]() .
.
(1)求椭圆的方程;
(2)若![]() 是椭圆上任意一点,
是椭圆上任意一点,![]() 为圆
为圆![]() 的任一直径,求
的任一直径,求![]() 的取值范围;
的取值范围;
(3)是否存在以椭圆上点![]() 为圆心的圆
为圆心的圆![]() ,使得过圆
,使得过圆![]() 上任意一点
上任意一点![]() 作圆
作圆![]() 的切线,切点为
的切线,切点为![]() ,都满足
,都满足![]() ?若存在,求出圆
?若存在,求出圆![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
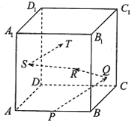
【题目】如图,在正方体![]() 中,棱
中,棱![]() 的中点为
的中点为![]() ,若光线从点
,若光线从点![]() 出发,依次经三个侧面
出发,依次经三个侧面![]() ,
,![]() ,
,![]() 反射后,落到侧面
反射后,落到侧面![]() (不包括边界),则入射光线
(不包括边界),则入射光线![]() 与侧面
与侧面![]() 所成角的正切值的范围是( )
所成角的正切值的范围是( )
A.![]() B.
B.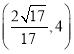 C.
C. D.
D.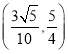
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“勾股定理”在西方被称为“毕达哥拉斯定理”,国时期吴国的数学家赵爽创制了一幅“勾股圆方图”,用数形结合的方法给出了勾股定理的详细证明![]() 如图所示的“勾股圆方图”中,四个相同的直角三角形与中间的小正方形拼成一个大正方形
如图所示的“勾股圆方图”中,四个相同的直角三角形与中间的小正方形拼成一个大正方形![]() 若直角三角形中较小的锐角
若直角三角形中较小的锐角![]() ,现在向该大止方形区域内随机地投掷一枚飞镖,则飞镖落在阴影部分的概率是
,现在向该大止方形区域内随机地投掷一枚飞镖,则飞镖落在阴影部分的概率是![]()
![]()

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,对于函数
,对于函数![]() 有下述四个结论:
有下述四个结论:
①函数![]() 在其定义域上为增函数;
在其定义域上为增函数;
②对于任意的![]() ,都有
,都有![]() 成立;
成立;
③![]() 有且仅有两个零点;
有且仅有两个零点;
④若![]() 在点
在点![]() 处的切线也是
处的切线也是![]() 的切线,则
的切线,则![]() 必是
必是![]() 零点.
零点.
其中所有正确的结论序号是( )
A.①②③B.①②C.②③④D.②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公园计划在矩形空地上建造一个扇形花园如图①所示,矩形![]() 的
的![]() 边与
边与![]() 边的长分别为48米与40米,扇形的圆心
边的长分别为48米与40米,扇形的圆心![]() 为
为![]() 中点,扇形的圆弧端点
中点,扇形的圆弧端点![]() ,
,![]() 分别在
分别在![]() 与
与![]() 上,圆弧的中点
上,圆弧的中点![]() 在
在![]() 上.
上.
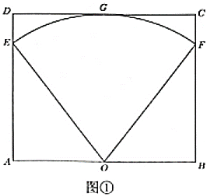
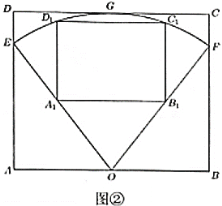
(1)求扇形花园的面积(精确到1平方米);
(2)若在扇形花园内开辟出一个矩形区域![]() 为花卉展览区.如图②所示,矩形
为花卉展览区.如图②所示,矩形![]() 的四条边与矩形
的四条边与矩形![]() 的对应边平行,点
的对应边平行,点![]() ,
,![]() 分别在
分别在![]() ,
,![]() 上,点
上,点![]() ,
,![]() 在扇形的弧上.某同学猜想:当矩形
在扇形的弧上.某同学猜想:当矩形![]() 面积最大时,两矩形
面积最大时,两矩形![]() 与
与![]() 的形状恰好相同(即长与宽之比相同),试求花卉展览区
的形状恰好相同(即长与宽之比相同),试求花卉展览区![]() 面积的最大值,并判断上述猜想是否正确(请说明理由).
面积的最大值,并判断上述猜想是否正确(请说明理由).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com