
已知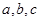 均为正数,证明:
均为正数,证明: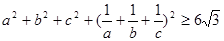 ,并确定
,并确定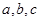 为何值时,等号成立。
为何值时,等号成立。
利用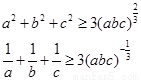 ①所以
①所以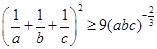 ② ……6分
② ……6分
故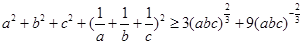 .
.
又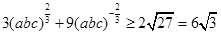 ③
③
(证法二)利用
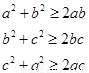 证明。
证明。
【解析】
试题分析:(证法一)因为a,b,c均为正数,由平均值不等式得
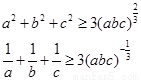 ①所以
①所以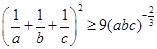 ② ……6分
② ……6分
故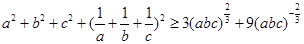 .
.
又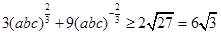 ③
③
所以原不等式成立. ……8分
当且仅当a=b=c时,①式和②式等号成立。当且仅当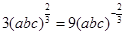 时,③式等号成立。即当且仅当a=b=c=
时,③式等号成立。即当且仅当a=b=c=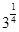 时,原式等号成立。 ……10分
时,原式等号成立。 ……10分
(证法二)因为a,b,c均为正数,由基本不等式得
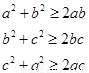
所以 ①
①
同理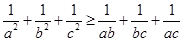 ② ……6分
② ……6分
故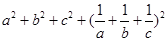
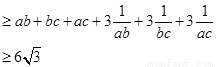 ③
③
所以原不等式成立. ……8分
当且仅当a=b=c时,①式和②式等号成立,当且仅当a=b=c,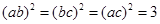 时,③式等号成立。
时,③式等号成立。
即当且仅当a=b=c=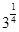 时,原式等号成立。 ……10分
时,原式等号成立。 ……10分
考点:本题主要考查简单不等式的证明。
点评:中档题,不等式的证明方法,通常有“综合法”、“分析法”“反证法”等,不等式的性质、基本不等式等基础知识,是不等式证明的基础,应牢记并灵活运用。本题证法较多,入口较易。


 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:高中数学 来源:2013届吉林省高二下学期期末理科数学试卷(解析版) 题型:解答题
(本小题满分10分)选修4-5:不等式选讲
已知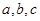 均为正数,证明:
均为正数,证明: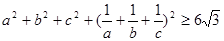 ,并确定
,并确定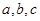 为何值时,等号成立。
为何值时,等号成立。
查看答案和解析>>
科目:高中数学 来源:2010-2011学年河南省高三上学期九月月考理科数学卷 题型:解答题
(本小题满分10分)选修4-5,不等式选讲
已知 均为正数,证明:
均为正数,证明: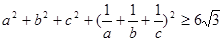 ,并确定
,并确定 为何值时,等号成立。
为何值时,等号成立。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com