
分析 (1)求出函数的导数,结合二次函数的性质判断导函数的符号,从而求出函数的单调区间;
(2)假设存在,根据x1+x2=2m,x1x2=1,得到消元得$ln\frac{1}{x_2}-ln{x_2}=\frac{1}{x_2}-{x_2}$,根据f(x)的单调性判断函数无零点,得出结论即可.
解答 解:(1)函数f(x)的定义域(0,+∞),
$f'(x)=\frac{{{x^2}-2mx+1}}{x^2}$,令h(x)=x2-2mx+1,
△=4m2-4=4(m2-1),
当△>0即m>1或m<-1时,方程h(x)=0有两个根,
设方程x2-2mx+1=0的两根是:x1,x2,且x1<x2,
解得:x1=m-$\sqrt{{m}^{2}-1}$,x2=m+$\sqrt{{m}^{2}-1}$,
∴x1+x2=m,x1•x2=1,
当△≤0时,即m∈[-1,1]时,f′(x)≥0,原函数在定义域上单调递增,
当m<-1时,△>0,两根均为负,f(x)在定义域上单调递增,
当m>1时,△>0,两根均为正,
故f(x)在区间(0,m-$\sqrt{{m}^{2}-1}$),(m+$\sqrt{{m}^{2}-1}$,+∞)递增,在(m-$\sqrt{{m}^{2}-1}$,m+$\sqrt{{m}^{2}-1}$)递减;
(2)由(1)知函数有两个极值点时m>1且x1+x2=2m,x1x2=1
AB斜率$k=\frac{{f({x_2})-f({x_1})}}{{{x_2}-{x_1}}}=2-2m\frac{{ln{x_1}-ln{x_2}}}{{{x_1}-{x_2}}}$,
若k=2-2m,则$\frac{{ln{x_1}-ln{x_2}}}{{{x_1}-{x_2}}}=1$,
两根均为正且x1x2=1,若x1<x2,则x1<1,x2>1,
消元得$ln\frac{1}{x_2}-ln{x_2}=\frac{1}{x_2}-{x_2}$,
整理得x2-$\frac{1}{{x}_{2}}$-2lnx2=0,
由(1)知$f(x)=x-\frac{1}{x}-2lnx$在区间(1,+∞)上单调递增,
因此f(x)>f(1)=0,函数没有零点,
故这样的m值不存在.
点评 本题考查了函数的单调性、最值问题,考查导数的应用,是一道综合题.


科目:高中数学 来源: 题型:选择题
 如图是抛物线形拱桥,当水面在时,拱顶离水面2m,水面宽4m,如果水位下降$\frac{5}{2}$m后(水深大于5m),水面宽度为( )
如图是抛物线形拱桥,当水面在时,拱顶离水面2m,水面宽4m,如果水位下降$\frac{5}{2}$m后(水深大于5m),水面宽度为( )| A. | 1m | B. | 6m | C. | $2\sqrt{5}$m | D. | 4m |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
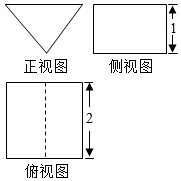 《九章算术》中,将底面是直角三角形的直三棱柱称之为“堑堵”,已知某“堑堵”的三视图如图所示,俯视图中虚线平分矩形的面积,则该“堑堵”的侧面积为( )
《九章算术》中,将底面是直角三角形的直三棱柱称之为“堑堵”,已知某“堑堵”的三视图如图所示,俯视图中虚线平分矩形的面积,则该“堑堵”的侧面积为( )| A. | 2 | B. | 4+2$\sqrt{2}$ | C. | 4+4$\sqrt{2}$ | D. | 6+4$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\frac{7}{2}$ | C. | 2 | D. | $\frac{7}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 欧巴老师布置给时镇同学这样一份数学作业:在同一个直角坐标系中画出四个对数函数的图象,使它们的底数分别为$\sqrt{3}$、$\frac{1}{10}$、e和$\frac{3}{5}$.时镇同学为了和暮烟同学出去玩,问大英同学借了作业本很快就抄好了,详见如图.第二天,欧巴老师当堂质问时镇同学:“你画的四条曲线中,哪条是底数为e的对数函数图象?”时镇同学无言以对,憋得满脸通红.眼看时镇同学就要被欧巴老师训斥一番,聪明睿智的你能不能帮他一把,回答这个问题呢?
欧巴老师布置给时镇同学这样一份数学作业:在同一个直角坐标系中画出四个对数函数的图象,使它们的底数分别为$\sqrt{3}$、$\frac{1}{10}$、e和$\frac{3}{5}$.时镇同学为了和暮烟同学出去玩,问大英同学借了作业本很快就抄好了,详见如图.第二天,欧巴老师当堂质问时镇同学:“你画的四条曲线中,哪条是底数为e的对数函数图象?”时镇同学无言以对,憋得满脸通红.眼看时镇同学就要被欧巴老师训斥一番,聪明睿智的你能不能帮他一把,回答这个问题呢?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com