ρ=4sinθ (-∞,1005)
分析:①圆C的普通方程为x
2+y
2=4y,由x
2+y
2=ρ
2,4y=4ρsinθ,能求出圆C的极坐标方程为 ρ=4sinθ.
②当x≥-a时,原式=x+2a+|x-1|<2011,当x>1时,2x+2a-1<2011,2x+2a<2012,a<1006-x<1005.当x=1时,1+2a<2011,a<1005.当x<1时,2a+1<2011,a<1005.当x<-a时,原式=|x-1|-x<2011,不等式恒成立.由此能求出a的取值范围.
解答:①∵圆C的参数方程为
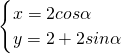
(α为参数),
∴圆C的普通方程为x
2+(y-2)
2=4,
即x
2+y
2=4y,
∵x
2+y
2=ρ
2,4y=4ρsinθ,
∴圆C的极坐标方程为 ρ=4sinθ.
故答案为:ρ=4sinθ.
②当x≥-a时,原式=x+2a+|x-1|<2011,
当x>1时,2x+2a-1<2011,
2x+2a<2012,
a<1006-x<1005.
当x=1时,1+2a<2011,
a<1005.
当x<1时,2a+1<2011,
a<1005.
当x<-a时,原式=|x-1|-x<2011,
不等式恒成立.
综上所述,a<1005.
故答案为:(-∞,1005).
点评:第①考查圆的参数方程、普通方程和极坐标方程的相互转化,是基础题.解题时要认真审题,注意合理地进行等价转化.
第②考查含参数的绝对值不等式的解法,是基础题.解题时要认真审题,注意分类讨论思想的灵活运用.

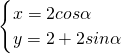 (α为参数),若以原点O为极点,以x轴正半轴为极轴建立极坐标系,则圆C的极坐标方程为________.
(α为参数),若以原点O为极点,以x轴正半轴为极轴建立极坐标系,则圆C的极坐标方程为________.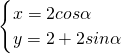 (α为参数),
(α为参数),

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 (2012•黄冈模拟)(选做题:请在下列两题中任选一题作答,如果多做,则按所做的第一题评分)
(2012•黄冈模拟)(选做题:请在下列两题中任选一题作答,如果多做,则按所做的第一题评分)