
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 Rt△ABC中,∠C=90°,CD⊥AB,AD为圆O的直径,圆O与AC交于E,求证:$\frac{AE}{CE}$=$\frac{A{C}^{2}}{B{C}^{2}}$.
Rt△ABC中,∠C=90°,CD⊥AB,AD为圆O的直径,圆O与AC交于E,求证:$\frac{AE}{CE}$=$\frac{A{C}^{2}}{B{C}^{2}}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (0,2) | C. | (1,+∞) | D. | (2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
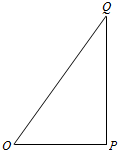 如图,O,P,Q三地有直道相通,OP=3千米,PQ=4千米,OQ=5千米,现甲、乙两警员同时从O地出发匀速前往Q地,经过t小时,他们之间的距离为f(t)(单位:千米).甲的路线是OQ,速度为5千米/小时,乙的路线是OPQ,速度为8千米/小时,乙到达Q地后在原地等待.设t=t1时乙到达P地,t=t2时乙到达Q地.
如图,O,P,Q三地有直道相通,OP=3千米,PQ=4千米,OQ=5千米,现甲、乙两警员同时从O地出发匀速前往Q地,经过t小时,他们之间的距离为f(t)(单位:千米).甲的路线是OQ,速度为5千米/小时,乙的路线是OPQ,速度为8千米/小时,乙到达Q地后在原地等待.设t=t1时乙到达P地,t=t2时乙到达Q地.查看答案和解析>>
科目:高中数学 来源:2017届河南商丘第一高级中学年高三上理开学摸底数学试卷(解析版) 题型:选择题
将函数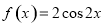 的图象向右平移
的图象向右平移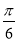 个单位后得到函数
个单位后得到函数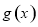 的图象.若函数
的图象.若函数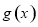 在区间
在区间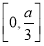 和
和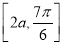 上均单调递增,则实数
上均单调递增,则实数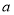 的取值范围是( )
的取值范围是( )
A. B.
B.
C.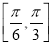 D.
D.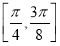
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
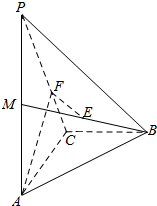 如图,在四面体P-ABC中,PA⊥面ACB,BC⊥AC,M是PA的中点,E是BM的中点,AC=2,PA=4,F是线段PC上的点,且EF∥面ACB.
如图,在四面体P-ABC中,PA⊥面ACB,BC⊥AC,M是PA的中点,E是BM的中点,AC=2,PA=4,F是线段PC上的点,且EF∥面ACB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com