
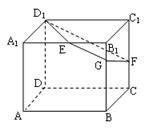
如图,已知正方体![]() 的棱长为2,E、F分别是
的棱长为2,E、F分别是![]() 、
、![]() 的中点,过
的中点,过![]() 、E、F作平面
、E、F作平面![]() 交
交![]() 于G..
于G..
(Ⅰ)求证:![]() ∥
∥![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)求正方体被平面![]() 所截得的几何体
所截得的几何体![]() 的体积.
的体积.
(Ⅰ)证明见解析, (Ⅱ)所成二面角的余弦值为![]() ,(Ⅲ)
,(Ⅲ)![]()
(Ⅰ)证明:在正方体![]() 中,∵平面
中,∵平面![]() ∥平面
∥平面![]()
平面![]()
![]() 平面
平面![]()
![]() ,平面
,平面![]()
![]() 平面
平面![]()
![]()
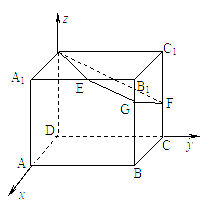 ∴
∴![]() ∥
∥![]() .-------------------------------------3分
.-------------------------------------3分
(Ⅱ)解:如图,以D为原点分别以DA、DC、DD1为
x、y、z轴,建立空间直角坐标系,则有
D1(0,0,2),E(2,1,2),F(0,2,1),
∴![]() ,
,![]()
设平面![]() 的法向量为
的法向量为 ![]()
则由![]() ,和
,和![]() ,得
,得![]() ,
,
取![]() ,得
,得![]() ,
,![]() ,∴
,∴![]() ------------------------------6分
------------------------------6分
又平面![]() 的法向量为
的法向量为![]() (0,0,2)
(0,0,2)
故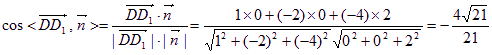 ;
;
∴截面![]() 与底面
与底面![]() 所成二面角的余弦值为
所成二面角的余弦值为![]() . ------------------9分
. ------------------9分
(Ⅲ)解:设所求几何体![]() 的体积为V,
的体积为V,
∵![]() ~
~![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
![]() --------------------------11分
--------------------------11分
故V棱台![]()
![]()
![]()
∴V=V正方体-V棱台![]()
![]() . ------------------14分
. ------------------14分


科目:高中数学 来源:2011届广东省汕头市高三四校联考数学理卷 题型:解答题
.(本小题满分14分)
如图,已知正方体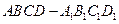 的棱长为2,E、F分别是
的棱长为2,E、F分别是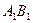 、
、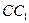 的中点,过
的中点,过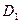 、E、F作平面
、E、F作平面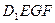 交
交 于G..
于G..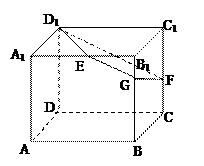
(Ⅰ)求证: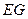 ∥
∥ ;
;
(Ⅱ)求二面角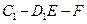 的余弦值;
的余弦值;
(Ⅲ)求正方体被平面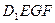
 所截得的几何体
所截得的几何体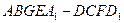 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源:2012年苏教版高中数学必修2 2.3空间直角坐标系练习卷(解析版) 题型:解答题
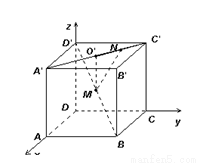
(14分)如图,已知正方体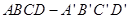 的棱长为a,M为
的棱长为a,M为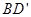 的中点,点N在
的中点,点N在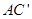 上,且
上,且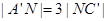 ,试求MN的长.
,试求MN的长.
查看答案和解析>>
科目:高中数学 来源:2010年上海市徐汇区高三第二次模拟考试数学卷(理) 题型:解答题
(本题满分14分)
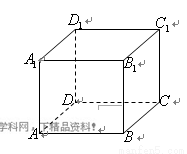
(如图)已知正方体 的棱长均为1,
的棱长均为1, 为棱
为棱 上的点,
上的点, 为棱
为棱 的中点,异面直线
的中点,异面直线 与
与 所成角的大小为
所成角的大小为 ,求
,求 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com