
在三棱柱 中,已知
中,已知 ,在
,在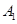 在底面
在底面 的投影是线段
的投影是线段 的中点
的中点 。
。

(1)求点C到平面 的距离;
的距离;
(2)求二面角 的余弦值;
的余弦值;
(3)若M,N分别为直线 上动点,求MN的最小值。
上动点,求MN的最小值。
(1) (2)
(2)
(3)异面直线 的距离
的距离 即为MN的最小值
即为MN的最小值
【解析】
试题分析:解:(1)连接AO, 因为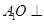 平面ABC,所以
平面ABC,所以 ,因为
,因为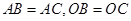 ,
,
得 ,
, 在
在 中,
中,
在 中,
中, 则
则 又
又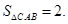
设点C到平面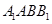 的距离为
的距离为
则由 得,
得,
 从而
从而 ……4分
……4分
(2)如图所示,分别以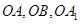 所在的直线 为x,y,z轴,建立空间直角坐标系,
所在的直线 为x,y,z轴,建立空间直角坐标系,

则A(1,0,0),
C(0,-2,0), A1(0.0,2),B(0,2,0),  ,
, .
.
设平面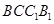 的法向量
的法向量 ,
,
又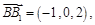

由 ,得
,得 ,
,
令 ,得
,得 ,即
,即 。
。
设平面 的法向量
的法向量 , 又
, 又

由 ,得
,得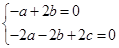 ,令
,令 ,得
,得 ,即
,即 。
。
所以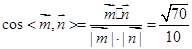 ,……7分
,……7分
由图形观察可知,二面角 为钝角,
为钝角,
所以二面角 的余弦值是
的余弦值是 .
……9分
.
……9分
(3)方法1.在 中,作
中,作 于点E,因为
于点E,因为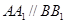 ,得
,得 .
.
因为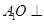 平面ABC,所以
平面ABC,所以 ,因为
,因为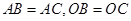 ,
,
得 ,所以
,所以 平面
平面 ,所以
,所以 ,
,
所以 平面
平面 .从而
.从而
在 中,
中,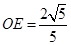 为异面直线
为异面直线 的距离,即为MN的最小值。……14分
的距离,即为MN的最小值。……14分
方法2.设向量 ,且
,且
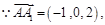


令 ,得
,得 ,即
,即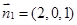 。
。
所以异面直线 的距离
的距离 即为MN的最小值。……14分
即为MN的最小值。……14分
考点:空间中点线面的位置关系
点评:解决的关键是熟练的根据空间中的线面垂直性质定理以及二面角的平面角的定义和异面直线距离的求解得到,属于基础题。


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
 如图,在三棱柱中,已知AB⊥侧面BB1C1C,AB=BC=1,BB1=2,∠BCC1=
如图,在三棱柱中,已知AB⊥侧面BB1C1C,AB=BC=1,BB1=2,∠BCC1=| π |
| 3 |
| π |
| 4 |
查看答案和解析>>
科目:高中数学 来源:2011届福建省莆田十中高三5月月考调理科数学 题型:解答题
(本题满分13分)
如图,在三棱 柱
柱 中,已知
中,已知
 ,
, 侧面
侧面
(1)求直线C1B与底面ABC所成角的正弦值;
(2)在棱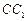 (不包含端点
(不包含端点 上确定一点
上确定一点 的位置,使得
的位置,使得 (要求说明理由).
(要求说明理由).
(3)在(2)的条件下,若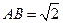 ,求二面角
,求二面角 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年福建省高三5月月考调理科数学 题型:解答题
(本题满分13分)
如图,在三棱柱 中,已知
中,已知
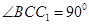 ,
,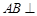 侧面
侧面
(1)求直线C1B与底面ABC所成角的正弦值;

(2)在棱 (不包含端点
(不包含端点 上确定一点
上确定一点 的位置,使得
的位置,使得 (要求说明理由).
(要求说明理由).
(3)在(2)的条件下,若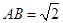 ,求二面角
,求二面角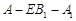 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源:2013届浙江省高二上学期八校联考理科数学 题型:解答题
(本小题满分15分)如图,在三棱柱 中,已知
中,已知 ,
,
 ,
, .
.
(Ⅰ)求直线 与底面
与底面 所成角正切值;
所成角正切值;
(Ⅱ)在棱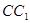 (不包含端点)上确定一点
(不包含端点)上确定一点 的位置,
的位置,
使得 (要求说明理由);
(要求说明理由);
(Ⅲ)在(Ⅱ)的条件下,若 ,求二面角
,求二面角 的大小.
的大小.

查看答案和解析>>
科目:高中数学 来源:2010年重庆市高三考前第一次模拟考试数学(理) 题型:填空题
如题13图,在正三棱柱 中,已知
中,已知 点
点 在棱
在棱 上,且
上,且 且
且 与平面
与平面 所成的角的正弦值是____________.
所成的角的正弦值是____________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com