
【题目】已知函数![]() 有三个极值点
有三个极值点![]() ,
,
(1)求实数![]() 的取值范围;
的取值范围;
(2)求证:![]() .
.
【答案】(1)![]() 且
且![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)函数![]() 有3个零点等价于
有3个零点等价于![]() 有3个变号零点,由于
有3个变号零点,由于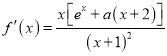 ,且
,且![]() ,所以可得
,所以可得![]() 有两个不为0,-1的实根,再对
有两个不为0,-1的实根,再对![]() 求导讨论其单调性可得结果;
求导讨论其单调性可得结果;
(2)由(1)可知![]() 有一个零点为0,所以不妨设
有一个零点为0,所以不妨设![]() ,
,![]() ,而
,而![]() ,所以
,所以![]() ,因此要证
,因此要证![]() ,即证
,即证![]() 而
而![]() ,
,![]() ,而
,而![]() 在
在![]() 上递减,
上递减,![]() ,所以只需证
,所以只需证![]() ,即
,即![]() ,然后构造函数
,然后构造函数![]() ,只需证此函数值恒大于零即可.
,只需证此函数值恒大于零即可.
解:(1)利用![]() 的极值点个数即为
的极值点个数即为![]() 的变号零点个数
的变号零点个数
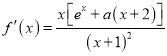 ,
,![]() ,设
,设![]() ,
,
由已知,方程![]() 有两个不为0,-1的实根,
有两个不为0,-1的实根,![]()
当![]() 时,
时,![]() 在
在![]() 上递增,
上递增,![]() 至多一个实根,故
至多一个实根,故![]()
所以![]() 在
在![]() 上递减,在
上递减,在![]() 上递增,
上递增,
因为![]() ,
,![]()
所以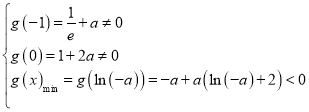 时,
时,![]() 有两个实根,
有两个实根,
解得![]() 且
且![]()
(2)由(1)不妨设![]() ,
,![]() ,∵
,∵![]() ,∴
,∴![]() .
.
要证![]() ,即证
,即证![]() 而
而![]() ,
,![]()
由![]() 在
在![]() 上递减,在
上递减,在![]() 上递增,且
上递增,且![]()
故只要证![]() ,又
,又![]() ,故只要证
,故只要证![]()
即证![]()
设![]()
∴![]()
∴![]() 递增,∴
递增,∴![]()
即![]()
∴![]()


科目:高中数学 来源: 题型:
【题目】已知点![]() 为抛物线
为抛物线![]() 的焦点,过点
的焦点,过点![]() 任作两条互相垂直的直线
任作两条互相垂直的直线![]() ,
,![]() ,分别交抛物线
,分别交抛物线![]() 于
于![]() ,
,![]() ,
,![]() ,
,![]() 四点,
四点,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点.
的中点.
(1)求证:直线![]() 过定点,并求出该定点的坐标;
过定点,并求出该定点的坐标;
(2)设直线![]() 交抛物线
交抛物线![]() 于
于![]() ,
,![]() 两点,试求
两点,试求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前n项和为
的前n项和为![]() ,
,![]()
![]() ,若
,若![]() 是公差不为0的等差数列,且
是公差不为0的等差数列,且![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)证明:数列![]() 是等差数列;
是等差数列;
(3)记![]() ,若存在
,若存在![]() ,
,![]() (
(![]() ),使得
),使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣a|+|x+2|.
(1)当a=1 时,求不等式f(x)≤5的解集;
(2)x0∈R,f(x0)≤|2a+1|,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,以原点
,以原点![]() 为圆心,椭圆
为圆心,椭圆![]() 的长半轴为半径的圆与直线
的长半轴为半径的圆与直线![]() 相切.
相切.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)已知点![]() ,
, ![]() 为动直线
为动直线![]() 与椭圆
与椭圆![]() 的两个交点,问:在
的两个交点,问:在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 为定值?若存在,试求出点
为定值?若存在,试求出点![]() 的坐标和定值,若不存在,请说明理由.
的坐标和定值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国在北宋年间(公元1084年)第一次印刷出版了《算经十书》,即贾宪的《黄帝九章算法细草》,刘益的《议古根源》,秦九韶的《数书九章》,李冶的《测圆海镜》和《益古演段》,杨辉的《详解九章算法》、《日用算法》和《杨辉算法》,朱世杰的《算学启蒙》和《四元玉鉴》.这些书中涉及的很多方面都达到古代数学的高峰,其中一些“算法”如开立方和开四次方也是当时世界数学的高峰,哈三中图书馆中正好有这十本书,但是书名中含有“算”字的书都已经借出,现在小张同学从剩余的书中任借两本阅读,那么他借到《数书九章》的概率为_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】稠环芳香烃化合物中有不少是致癌物质,比如学生钟爱的快餐油炸食品中会产生苯并芘,它是由一个苯环和一个芘分子结合而成的稠环芳香烃类化合物,长期食用会致癌.下面是一组稠环芳香烃的结构简式和分子式:
名称 | 萘 | 蒽 | 并四苯 | … | 并n苯 |
结构简式 |
|
|
| … | … |
分子式 |
|
|
| … | … |
由此推断并十苯的分子式为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一款小游戏的规则如下:每轮游戏要进行三次,每次游戏都需要从装有大小相同的2个红球,3个白球的袋中随机摸出2个球,若摸出的“两个都是红球”出现3次获得200分,若摸出“两个都是红球”出现1次或2次获得20分,若摸出“两个都是红球”出现0次则扣除10分(即获得![]() 分).
分).
(1)设每轮游戏中出现“摸出两个都是红球”的次数为![]() ,求
,求![]() 的分布列;
的分布列;
(2)玩过这款游戏的许多人发现,若干轮游戏后,与最初的分数相比,分数没有增加反而减少了,请运用概率统计的相关知识分析解释上述现象.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com