
(本小题12分) 正项数列{an}满足a1=2,点An(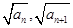 )在双曲线y2-x2=1上,点(
)在双曲线y2-x2=1上,点(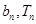 )在直线y=-
)在直线y=-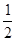 x+1上,其中Tn是数列{bn}的前n项和。
x+1上,其中Tn是数列{bn}的前n项和。
①求数列{an}、{bn}的通项公式;
②设Cn=anbn,证明 Cn+1<Cn
③若m-7anbn>0恒成立,求正整数m的最小值。
(1) an=n+1,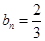
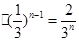 (2)利用单调性法加以证明。
(2)利用单调性法加以证明。
(3) m的最小值为10
解析试题分析:① 由已知点An在y2-x2=1上知,an+1-an=1,
∴数列{an}是一个以2为首项,以1为公差的等差数列。
∴an=n+1
∵点(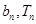 )在直线y=-
)在直线y=-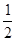 x+1上
x+1上
∴Tn=-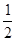 bn+1 ①
bn+1 ①
∴Tn-1=-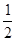 bn-1+1 ②
bn-1+1 ②
①②两式相减得bn=-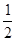 bn+
bn+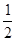 bn-1
bn-1
∴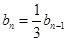
令n=1得 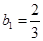
∴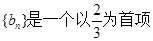 ,
, 。
。
∴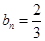
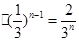
②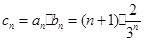
∴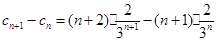
=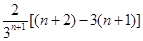
=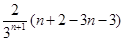
=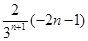 <0,
<0,
∴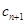 <
<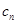
③ ∵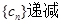 而m>7
而m>7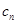 恒成立 ∴m>7c1=
恒成立 ∴m>7c1=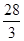 而
而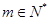
∴m的最小值为10。
考点:本试题考查了数列的通项公式和前n项和的求解运用。
点评:对于数列图像的求解,该试题以函数为背景建立了递推关系式,进而得到是等差数列,同时能借助于通项公式与前n项和的关系式,整体的思想求解通项公式,这是重要的一点。而对于错位相减法求和需要熟练掌握,找到容易出错的细节就是最后一步的合并,要细心点,属于中档题。


科目:高中数学 来源: 题型:解答题
(本题满分14分)
对数列{an},规定{△an}为数列{an}的一阶差分数列,其中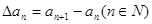 。
。
对自然数k,规定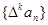 为{an}的k阶差分数列,其中
为{an}的k阶差分数列,其中 。
。
(1)已知数列{an}的通项公式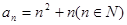 ,试判断
,试判断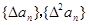 是否为等差或等比数列,为什么?
是否为等差或等比数列,为什么?
(2)若数列{an}首项a1=1,且满足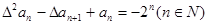 ,求数列{an}的通项公式。
,求数列{an}的通项公式。
(3)对(2)中数列{an},是否存在等差数列{bn},使得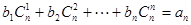 对一切自然
对一切自然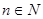 都成立?若存在,求数列{bn}的通项公式;若不存在,则请说明理由。
都成立?若存在,求数列{bn}的通项公式;若不存在,则请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)在数列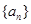 中,
中,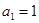 ,并且对于任意n∈N*,都有
,并且对于任意n∈N*,都有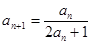 .
.
(1)证明数列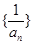 为等差数列,并求
为等差数列,并求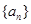 的通项公式;
的通项公式;
(2)设数列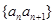 的前n项和为
的前n项和为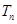 ,求使得
,求使得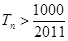 的最小正整数
的最小正整数 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com