
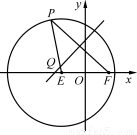
如图,已知圆E: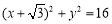 ,点
,点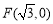 ,P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q.
,P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q.
(1)求动点Q的轨迹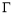 的方程;
的方程;
(2)已知A,B,C是轨迹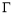 的三个动点,A与B关于原点对称,且
的三个动点,A与B关于原点对称,且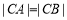 ,问△ABC的面积是否存在最小值?若存在,求出此时点C的坐标,若不存在,请说明理由.
,问△ABC的面积是否存在最小值?若存在,求出此时点C的坐标,若不存在,请说明理由.
(1)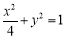 ;(2)存在最小值.点C的坐标为
;(2)存在最小值.点C的坐标为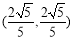 ,
, ,
,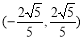 ,
,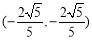
【解析】
试题分析:(1)连结QF,由于线段的垂直平分线上的点到线段两端点的距离相等,所以|QE|+|QF|=|QE|+|QP|=4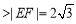 ,根据椭圆的定义知,动点Q的轨迹
,根据椭圆的定义知,动点Q的轨迹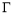 是以E,F为焦点,长轴长为4的椭圆.由此便可得其方程;(2)首先考虑直线AB的斜率为0或斜率不存在的情况,此时易得
是以E,F为焦点,长轴长为4的椭圆.由此便可得其方程;(2)首先考虑直线AB的斜率为0或斜率不存在的情况,此时易得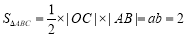 .当直线AB的斜率存在且不为0时,设斜率为k,则直线AB的直线方程为
.当直线AB的斜率存在且不为0时,设斜率为k,则直线AB的直线方程为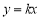 ,将△ABC的面积用含k的式子表示出来,然后利用重要不等式求其最小值.
,将△ABC的面积用含k的式子表示出来,然后利用重要不等式求其最小值.
(1)连结QF,根据题意,|QP|=|QF|,则|QE|+|QF|=|QE|+|QP|=4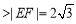 ,
,
故动点Q的轨迹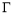 是以E,F为焦点,长轴长为4的椭圆. 2分
是以E,F为焦点,长轴长为4的椭圆. 2分
设其方程为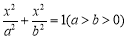 ,可知
,可知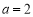 ,
,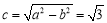 ,则
,则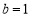 , 3分
, 3分
所以点Q的轨迹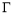 的方程为为
的方程为为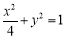 . 4分
. 4分
(2)存在最小值. 5分
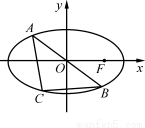
(ⅰ)当AB为长轴(或短轴)时,可知点C就是椭圆的上、下顶点(或左、右顶点),则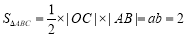 . 6分
. 6分
(ⅱ)方法一、当直线AB的斜率存在且不为0时,设斜率为k,则直线AB的直线方程为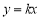 ,设点
,设点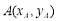 ,
,
联立方程组 消去y得
消去y得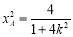 ,
,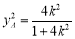 ,
,
由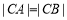 ,知△ABC是等腰三角形,O为AB的中点,则OC⊥AB,可知直线OC的方程为
,知△ABC是等腰三角形,O为AB的中点,则OC⊥AB,可知直线OC的方程为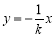 ,同理可得点C的坐标满足
,同理可得点C的坐标满足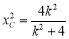 ,
,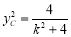 ,则
,则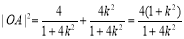 ,
,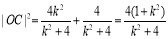 , 8分
, 8分
则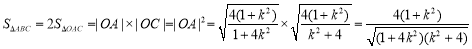 . 9分
. 9分
由于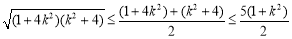 ,
,
所以 ,当且仅当
,当且仅当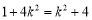 ,即
,即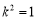 时取等号.
时取等号.
综合(ⅰ)(ⅱ),当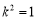 时,△ABC的面积取最小值
时,△ABC的面积取最小值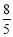 , 11分
, 11分
此时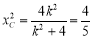 ,
, ,即
,即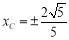 ,
,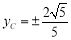 ,
,
所以点C的坐标为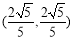 ,
, ,
,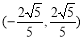 ,
,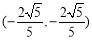 . 13分
. 13分
方法二、前同(ⅰ),记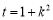 ,则
,则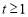 ,所以
,所以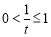 ,
,
故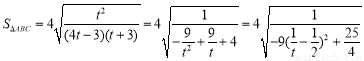 ,
,
当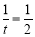 ,即
,即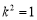 时,
时,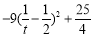 有最大值
有最大值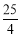 ,此时
,此时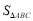 取得最小值
取得最小值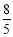 .
.
综合(ⅰ)(ⅱ),当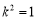 时,△ABC的面积取得最小值
时,△ABC的面积取得最小值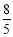 . 11分
. 11分
此时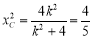 ,
,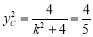 ,即
,即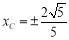 ,
,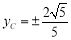 ,
,
所以点C的坐标为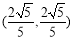 ,
, ,
,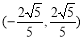 ,
,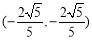 . 13分
. 13分
方法三、设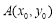 ,
,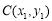 ,根据A,B两点关于原点对称,
,根据A,B两点关于原点对称,
则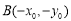 ,所以
,所以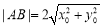 ,
,
由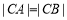 ,知△ABC是等腰三角形,O为AB的中点,则OC⊥AB,
,知△ABC是等腰三角形,O为AB的中点,则OC⊥AB,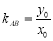 ,
,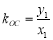 ,
,
由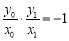 , ①
, ①
且点C在椭圆上,则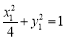 ②
②
联立①②,解得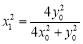 ,
,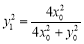 ,所以
,所以 , 8分
, 8分
所以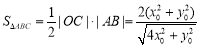 , 9分
, 9分
又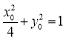 ,即
,即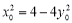 ,所以
,所以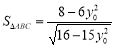 ,
,
记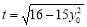 ,
,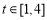 ,
,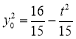 ,
,
则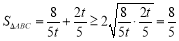 ,当且仅当
,当且仅当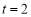 ,即
,即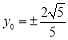 时等号成立,
时等号成立,
综合(ⅰ)(ⅱ),当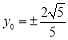 时,
时,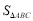 有最小值
有最小值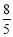 . 11分
. 11分
所以点C的坐标为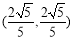 ,
, ,
,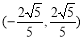 ,
,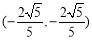 . 13分
. 13分
考点:1、椭圆的方程;2、直线与椭圆的关系;3、最值问题.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:高中数学 来源:2013-2014学年四川省高三下学期3月月考理科数学试卷(解析版) 题型:选择题
已知双曲线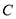 :
: (
(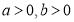 )的离心率为
)的离心率为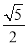 ,则
,则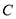 的渐近线方程为( )
的渐近线方程为( )
A. B.
B. C.
C.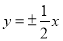 D.
D.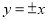
查看答案和解析>>
科目:高中数学 来源:2013-2014学年四川省资阳市高三下学期4月高考模拟考试理科数学试卷(解析版) 题型:填空题
设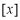 表示不超过
表示不超过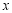 的最大整数,如
的最大整数,如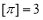 ,
,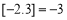 .给出下列命题:
.给出下列命题:
①对任意实数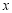 ,都有
,都有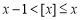 ;
;
②对任意实数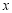 ,y,都有
,y,都有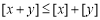 ;
;
③ ;
;
④若函数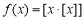 ,当
,当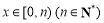 时,令
时,令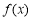 的值域为A,记集合A的元素个数为
的值域为A,记集合A的元素个数为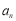 ,则
,则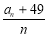 的最小值为
的最小值为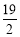 .
.
其中所有真命题的序号是_________________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年四川省资阳市高三下学期4月高考模拟考试理科数学试卷(解析版) 题型:选择题
已知实数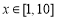 ,执行如图所示的程序框图,则输出x的值不小于55的概率为( )
,执行如图所示的程序框图,则输出x的值不小于55的概率为( )
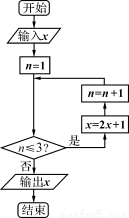
(A)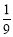 (B)
(B)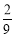 (C)
(C)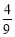 (D)
(D)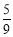
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com