
分析 可将P,A,B,C,D补全为长方体ABCD-A′B′C′D′,让P与A′重合,则该长方体的对角线PC即为球O的直径(球O为该长方体的外接球),于是可求得PC的长度,进一步可求出底面边长,从而求几何体P-ABCD的体积.
解答 解:依题意,可将P,A,B,C,D补全为长方体ABCD-A′B′C′D′,让P与A′重合,
则球O为该长方体的外接球,长方体的对角线PC即为球O的直径.
设ABCD是边长为a,PA⊥平面ABCD,PA=2,
∴PC2=AP2+2AB2=4+2a2=42,
∴a2=8,
则几何体P-ABCD的体积为V=$\frac{1}{3}$×a2×PA=$\frac{16}{3}$.
故答案为:$\frac{16}{3}$.
点评 本题考查直线与平面垂直的性质,考查球内接多面体的应用,“补形”是关键,考查分析、转化与运算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2017届湖北襄阳四中高三七月周考三数学(理)试卷(解析版) 题型:选择题
已知集合A={x|x+2>0},集合B={-3,-2,0,2},那么(CRA)∩B=( )
A. B.{-3,-2} C.{-3} D.{-2,0,2}
B.{-3,-2} C.{-3} D.{-2,0,2}
查看答案和解析>>
科目:高中数学 来源:2017届河南新乡一中高三9月月考数学(文)试卷(解析版) 题型:选择题
已知函数 ,则要得到其导函数
,则要得到其导函数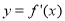 的图象,只需将函数
的图象,只需将函数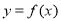 的图象( )
的图象( )
A.向右平移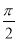 个单位
个单位
B.向左平移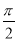 个单位
个单位
C.向右平移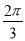 个单位
个单位
D.左平移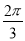 个单位
个单位
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
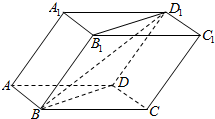 已知斜四棱柱ABCD-A1B1C1D1的各棱长均为2,∠A1AD=60°,∠BAD=90°,平面A1ADD1⊥平面ABCD,则直线BD1与平面ABCD所成的角的正切值为( )
已知斜四棱柱ABCD-A1B1C1D1的各棱长均为2,∠A1AD=60°,∠BAD=90°,平面A1ADD1⊥平面ABCD,则直线BD1与平面ABCD所成的角的正切值为( )| A. | $\frac{\sqrt{3}}{4}$ | B. | $\frac{\sqrt{13}}{4}$ | C. | $\frac{\sqrt{39}}{13}$ | D. | $\frac{\sqrt{39}}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com