

图7
活动:教师可引导学生思考探究,上例利用向量的几何法简捷地解决了平面几何问题.可否利用向量的坐标运算呢?这需要建立平面直角坐标系,找出所需点的坐标.如果能比较方便地建立起平面直角坐标系,如本例中图形,很方便建立平面直角坐标系,且图形中的各个点的坐标也容易写出,是否利用向量的坐标运算能更快捷地解决问题呢?教师引导学生建系、找点的坐标,然后让学生独立完成.
解:建立如图7所示的平面直角坐标系,取A(0,a),C(c,0),则B(-c,0),
![]() =(0,a),
=(0,a),![]() =(c,a),
=(c,a),![]() =(c,0),
=(c,0),![]() =(2c,0).
=(2c,0).
因为BB′、CC′都是中线,所以![]() =
=![]() (
(![]() +
+![]() )=
)=![]() [(2c,0)+(c,a)]=(
[(2c,0)+(c,a)]=(![]() ).
).
同理,![]() =(-
=(-![]() ).
).
因为BB′⊥CC′,所以-![]() =0,a2=9c2.
=0,a2=9c2.
所以cosA=![]() .
.
点评:比较是最好的学习方法.本例利用的方法与例题1有所不同,但其本质是一致的,教学中引导学生仔细体会这一点,比较两例的异同,找出其内在的联系,以达到融会贯通、灵活运用之功效.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案科目:高中数学 来源:学习周报 数学 人教课标高一版(A必修1) 2009-2010学年 第2期 总158期 人教课标高一版 题型:044
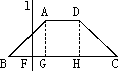
如图,已知底角为45°的等腰梯形ABCD,底边BC长为7 cm,腰长为2![]() cm,当一条垂直于底边BC(垂足为F)的直线l从左至右移动(与梯形ABCD有两个公共点)时,直线l把梯形分成两部分,令BF=x,试写出梯形在直线l左边部分的面积y关于x的函数解析式.
cm,当一条垂直于底边BC(垂足为F)的直线l从左至右移动(与梯形ABCD有两个公共点)时,直线l把梯形分成两部分,令BF=x,试写出梯形在直线l左边部分的面积y关于x的函数解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com