Question

14．某校高-年级举行语、数、英三科竞赛．高一（2）班共有32名同学参加三科竞赛．有16人参加语文竞赛，有10人参加数学竞赛，有16人参加英语竞赛，同时 参加语文竞赛和数学竞赛的有3人．同时参加语文竞赛和英语竞赛的有3人．没有人同时参加全部三科竞赛．问：同时参加数学竞赛和英语竞赛的有多少人？只参加语文竞赛的有多少人？

Answer 1

分析 设只参加语文竞赛的有x人，只参加数学竞赛的有y人，只参加英语竞赛的有z人，同时参加数学竞赛和英语竞赛的有p人，结合已知画出满足条件的图形，数形结合构造方程组，解得答案．

解答 解：如下图所示：
设只参加语文竞赛的有x人，只参加数学竞赛的有y人，只参加英语竞赛的有z人，
同时参加数学竞赛和英语竞赛的有p人，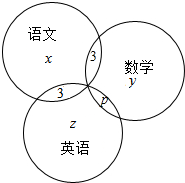

则有：x+y+z+p+3+3=32，
x+3+3=16，
y+p+3=10，
z+p+3=16，
解得：x=10，p=4，
即同时参加数学竞赛和英语竞赛的有4人，只参加语文竞赛的有10人．

点评 本题考查的知识点是Venn图表达集合的关系及运算，根据已知画出满足条件的图形，数形结合构造方程组，是解答的关键．