
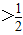 ;
; (-
(- -
-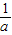 ),将其化简成关于x1、x2的式子即可证出m
),将其化简成关于x1、x2的式子即可证出m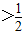 ;
;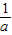 >0,故x1、x2同号.结合题意0<x1<2且|x1-x2|=2,证出x2=x1+2>2,从而得到2∈(x1,x2),由g(2)<0,即可证出4a+2b<1;
>0,故x1、x2同号.结合题意0<x1<2且|x1-x2|=2,证出x2=x1+2>2,从而得到2∈(x1,x2),由g(2)<0,即可证出4a+2b<1;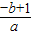 ,x1x2=
,x1x2=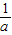 .设α<β,将2(α-x1)(β-x2)展开化简,进行配凑得2(α-x1)(β-x2)>2αβ-(x1+x2)(α+β)+2x1x2,结合2αβ-(x1+x2)(α+β)+2x1x2=
.设α<β,将2(α-x1)(β-x2)展开化简,进行配凑得2(α-x1)(β-x2)>2αβ-(x1+x2)(α+β)+2x1x2,结合2αβ-(x1+x2)(α+β)+2x1x2=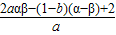 ,可得
,可得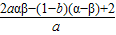 <0,结合a>0即可得到原不等式成立.
<0,结合a>0即可得到原不等式成立.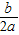 ,也就是x=
,也就是x= (-
(-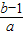 -
-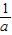 )
) (-
(-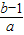 -
-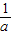 )=
)= (x1+x2)-
(x1+x2)- x1x2>
x1x2> (x1+x2)-
(x1+x2)- [(x1+x2)-1]=
[(x1+x2)-1]=
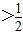 成立;
成立;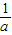 >0,故x1、x2同号
>0,故x1、x2同号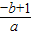 ,x1x2=
,x1x2=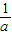
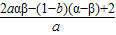
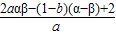 ,
,

科目:高中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 1 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com