
某高校在2012年自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100]得到的频率分布直方图如图所示.
(1)分别求第3,4,5组的频率;
(2)若该校决定在笔试成绩较高的第3,4,5组中用分层抽样抽取6名学生进入第二轮面试,
(ⅰ)已知学生甲和学生乙的成绩均在第三组,求学生甲和学生乙恰有一人进入第二轮面试的概率;
(ⅱ)学校决定在这已抽取到的6名学生中随机抽取2名学生接受考官L的面试,设第4组中有 名学生被考官L面试,求
名学生被考官L面试,求 的分布列和数学期望.
的分布列和数学期望.
(1)0.3 0.2 0.1 (2)  (3)
(3)
解析试题分析: (1)由频率分布直方图的横坐标得到组距,纵坐标得到每组的频率/组距,故而每组的频率即为纵坐标与组距的乘积.
(2)分层抽样就是在保持每个个体入样的可能性相等的条件下把样本容量分摊到每一层,即样本容量与总体数量之比与某层抽样个数与该层总数之比相等,进而得到每层抽样的人数
(i)第三组要抽样3人,在30人中抽样三人,无序即为组合数,即 中抽样情况,根据题目要求“学生甲和学生乙恰有一人进入第二轮面试”的事件分为两种情况①甲乙中只有甲入选,即还需要在28人中无序抽样2人,即
中抽样情况,根据题目要求“学生甲和学生乙恰有一人进入第二轮面试”的事件分为两种情况①甲乙中只有甲入选,即还需要在28人中无序抽样2人,即 ,②甲乙中只有乙入选,即还需要在28人中无序抽样2人,即
,②甲乙中只有乙入选,即还需要在28人中无序抽样2人,即 .在利用古典概型概率计算公式即可得到相应的概率
.在利用古典概型概率计算公式即可得到相应的概率
(ii)由分层抽样的结果可知6人中有两人是第四组的,即 ,再利用组合数算得从6人中无序抽样两人的情况数和分别有0,1,2人是第四组的情况数,即可得到相应的概率,进而得到分布列,在把三种情况的概率与其
,再利用组合数算得从6人中无序抽样两人的情况数和分别有0,1,2人是第四组的情况数,即可得到相应的概率,进而得到分布列,在把三种情况的概率与其 分别相乘再相加即可得到期望.
分别相乘再相加即可得到期望.
试题解析:(1)第三组的频率为0.06 5="0.3;" 第四组的频率为0.04
5="0.3;" 第四组的频率为0.04 5=0.2;第五组的频率为0.02
5=0.2;第五组的频率为0.02 5=0.1. 3分
5=0.1. 3分
(2)(ⅰ)设“学生甲和学生乙恰有一人进入第二轮面试”为事件A,第三组应有3人进入面试则:P(A)= =
= 6分
6分
(ⅱ)第四组应有2人进入面试,则随机变量 可能的取值为0,1,2. 7分
可能的取值为0,1,2. 7分
且 ,则随机变量
,则随机变量 的分布列为:
的分布列为:
10分
0 1 2 P 



12分
考点:分布列 期望 排列组合 频率分布直方图


科目:高中数学 来源: 题型:解答题
农科院的专家为了了解新培育的甲、乙两种麦苗的长势情况,从甲、乙两种麦苗的试验田中各抽取6株麦苗测量麦苗的株高,数据如下:(单位: )
)
甲:9,10,11,12,10,20
乙:8,14,13,10,12,21.
(1)在上面给出的方框内绘出所抽取的甲、乙两种麦苗株高的茎叶图;
(2)分别计算所抽取的甲、乙两种麦苗株高的平均数与方差,并由此判断甲、乙两种麦苗的长势情况.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了了解某年段1000名学生的百米成绩情况,随机抽取了若干学生的百米成绩,成绩全部介于13秒与18秒之间,将成绩按如下方式分成五组:第一组[13,14);第二组[14,15);……;第五组[17,18].按上述分组方法得到的频率分布直方图如图3所示,已知图中从左到右的前3个组的频率之比为3∶8∶19,且第二组的频数为8.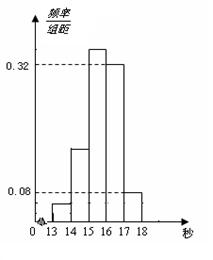
(1)将频率当作概率,请估计该年段学生中百米成绩在[16,17)内的人数;
(2)求调查中随机抽取了多少个学生的百米成绩;
(3)若从第一、五组中随机取出两个成绩,求这两个成绩的差的绝对值大于1秒的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
经销商经销某种农产品,在一个销售季度内,每售出 t该产品获利润
t该产品获利润 元,未售出的产品,每
元,未售出的产品,每 t亏损
t亏损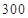 元。根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示。经销商为下一个销售季度购进了
元。根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示。经销商为下一个销售季度购进了 t该农产品,以
t该农产品,以 (单位:t,
(单位:t,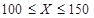 )表示下一个销售季度内的市场需求量,
)表示下一个销售季度内的市场需求量,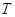 (单位:元)表示下一个销售季度内销商该农产品的利润。
(单位:元)表示下一个销售季度内销商该农产品的利润。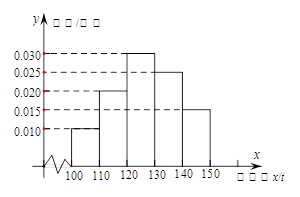
(1)将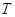 表示为
表示为 的函数;
的函数;
(2)根据直方图估计利润 不少于57000元的概率;
不少于57000元的概率;
(3)在直方图的需求量分组中,以各组的区间中点值代表该组的各个值,并以需求量落入该区间的频率作为需求量取该区间中点值的概率(例如:若 ,则取
,则取 ,且
,且 的概率等于需求量落入
的概率等于需求量落入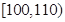 的概率),求利润
的概率),求利润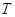 的数学期望.
的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
交通指数是交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念,记交通指数为T.其范围为[0,10],分别有五个级别:T∈[0,2)畅通;T∈[2,4)基本畅通; T∈[4,6)轻度拥堵; T∈[6,
8)中度拥堵;T∈[8,10]严重拥堵,晚高峰时段,从某市交通指挥中心选取了市区20个交通路段,依据其交通指数数据绘制直方图如图所示.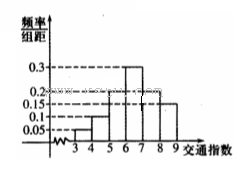
(1)这20个路段轻度拥堵、中度拥堵的路段各有多少个?
(2)从这20个路段中随机抽出的3个路段,用X表示抽取的中度拥堵的路段的个数,求X的分布列及期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某班高一某班的一次数学测试成绩的茎叶图和频率分布图都受到不同程度的破坏,但可见部分如下,据此解答如下问题:
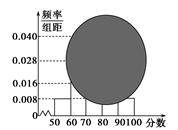
(1)求分数在[50,60)的频率及全班人数;
(2)求分数在[80,90)之间的频数,并计算频率分布直方图中[80,90)间的矩形的高;
(3)若要从分数在[80,100]之间的试卷中任取两份分析学生失分情况,在抽取的试卷中,求至少有一份分数在[90,100]之间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
由某种设备的使用年限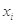 (年)与所支出的维修费
(年)与所支出的维修费 (万元)的数据资料,算得
(万元)的数据资料,算得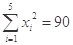 ,
, ,
, ,
,  .
.
(Ⅰ)求所支出的维修费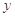 对使用年限
对使用年限 的线性回归方程
的线性回归方程 ;
;
(Ⅱ)判断变量 与
与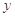 之间是正相关还是负相关;
之间是正相关还是负相关;
(Ⅲ)估计使用年限为8年时,支出的维修费约是多少.
附:在线性回归方程 中,
中, ,
, ,其中
,其中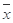 ,
, 为
为
样本平均值,线性回归方程也可写为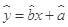 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
2013年9月20日是第25个全国爱牙日。某区卫生部门成立了调查小组,调查 “常吃零食与患龋齿的关系”,对该区六年级800名学生进行检查,按患龋齿和不患龋齿分类,得汇总数据:不常吃零食且不患龋齿的学生有60名,常吃零食但不患龋齿的学生有100名,不常吃零食但患龋齿的学生有140名.
 | 0.010 | 0.005 | 0.001 |
 | 6.635 | 7.879 | 10.828 |

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在每年的春节后,某市政府都会发动公务员参与到植树活动中去.为保证树苗的质量,该市林管部门在植树前,都会在植树前对树苗进行检测.现从甲乙两种树苗中各抽测了10株树苗的高度,量出树苗的高度如下(单位:厘米):
甲:
乙: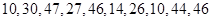
(1)根据抽测结果,完成答题卷中的茎叶图,并根据你填写的茎叶图,对甲、乙两种树苗的高度作比较,写出两个统计结论;
(2)设抽测的10株甲种树苗高度平均值为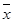 ,将这10株树苗的高度依次输入按程序框图进行的运算,问输出的
,将这10株树苗的高度依次输入按程序框图进行的运算,问输出的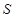 大小为多少?并说明
大小为多少?并说明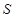 的统计学意义.
的统计学意义.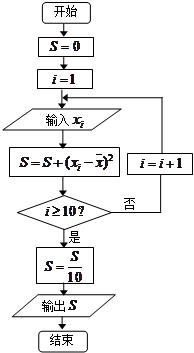
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com