
(本小题满分10分)
已知 ,
,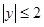 ,点
,点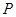 的坐标为
的坐标为
(1)当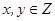 时,求
时,求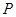 的坐标满足
的坐标满足 的概率。
的概率。
(2)当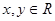 时,求
时,求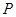 的坐标满足
的坐标满足 的概率。
的概率。
(1)
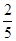 (2)
(2)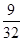
【解析】
试题分析:解:由 得
得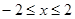 ,由
,由
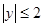 得
得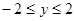 ,
,
(1)当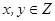 时,这是一个古典概型
时,这是一个古典概型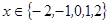 ,
,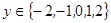 ………1分
………1分
总的基本事件个数是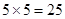 种。……………………… …………………… ……1分
种。……………………… …………………… ……1分
记“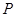 的坐标满足
的坐标满足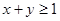 ”为事件
”为事件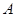
事件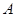 包含的基本事件有
包含的基本事件有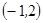 ,
,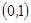 ,
,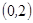 ,
,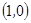 ,
,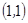 ,
,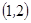 ,
,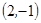
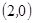 ,
,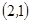 ,
,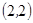 共10种。……………………………………………………2分
共10种。……………………………………………………2分
由古典概型的概率公式得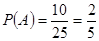 ………
……………… …………1分
………
……………… …………1分
(2)当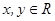 时,这是一个几何概型
时,这是一个几何概型
试验的全部结果构成的区域为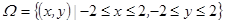
表示平面上的面积为 …… …1分
…… …1分
记“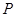 的坐标满足
的坐标满足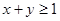 ”为事件
”为事件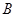 ………1分
………1分
所构成的区域为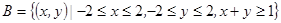
即右图阴影部分

面积为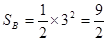 …… …… ………2分
…… …… ………2分
所以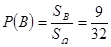 … …… ………………1分
… …… ………………1分
考点:本试题主要是考查了古典概型和几何概型概率的求解运用。
点评:通过该试题的解答明确了对这两个模型的准确选择,同时能利用各自的事件空间和事件发生的空间来求解概率的值,属于基础题。


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
 (选做题)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,若多做,则按作答的前两题评分,解答时应写出文字说明、证明过程或演算步骤.
(选做题)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,若多做,则按作答的前两题评分,解答时应写出文字说明、证明过程或演算步骤.
|
|
| 1 |
| 2a |
| 1 |
| 2b |
| 1 |
| 2c |
| 1 |
| b+c |
| 1 |
| c+a |
| 1 |
| a+b |
查看答案和解析>>
科目:高中数学 来源: 题型:
 本题包括(1)、(2)、(3)、(4)四小题,请选定其中两题,并在答题卡指定区域内答,
本题包括(1)、(2)、(3)、(4)四小题,请选定其中两题,并在答题卡指定区域内答,
|
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com