解:(1)函数的定义域是(0,+∞)

当a=-1时,f
′(x)=lnx+2
令f
′(x)=lnx+2>0,得

令f
′(x)=lnx+2<0,得

∴函数的单调递增区间是

函数的单调递减区间是

(2)∵对一切x∈(0,+∞),f(x)≥g(x)恒成立,
∴对一切x∈(0,+∞),xlnx-ax≥-x
2-2恒成立.
即对一切x∈(0,+∞),
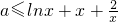
恒成立.
令

∵

∴当0<x<1时,F
′(x)<0,函数递减,当x>1时,F
′(x)>0,函数递增.
∴F(x)在x=1处取极小值,也是最小值,即F
min(x)=F(1)=3
∴a≤3
(3)证明:对一切x∈(0,+∞),都有
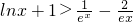
成立.
等价于证明:对一切x∈(0,+∞),都有

成立.
由(1)知,当a=-1时f(x)=xlnx+x,

令

,

当x∈(0,1)时,G
′(x)>0,函数G(x)递增,当x∈(1,+∞)时,G
′(x)<0,函数G(x)递减.f(x)
min>G(x)
max∴当x=1时,函数G(x)取到极大值,也是最大值.
∴

∵-

∴f(x)
min>G(x)
max∴对一切x∈(0,+∞),都有
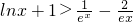
成立.
分析:(1)求出函数的导函数,当a=-1时,f
′(x)=lnx+2,令f
′(x)=lnx+2>0,得函数的单调递增区间是

,令f
′(x)=lnx+2<0,得函数的单调递减区间是

(2)把f(x)≥g(x)恒成立转化为对一切x∈(0,+∞),
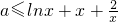
恒成立,构造函数

,研究F(x)的最小值;
(3)要证不等式在一个区间上恒成立,结合(1)把问题进行等价变形,研究函数f(x)的最小值和函数G(x)的最大值进行比较即可.
点评:本题主要考查了用导数研究函数的单调性和最大值,恒成立问题中用到了转化的数学思想.

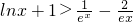 成立.
成立.




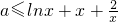 恒成立.
恒成立.

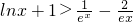 成立.
成立. 成立.
成立.
 ,
,


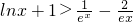 成立.
成立. ,令f′(x)=lnx+2<0,得函数的单调递减区间是
,令f′(x)=lnx+2<0,得函数的单调递减区间是
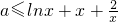 恒成立,构造函数
恒成立,构造函数 ,研究F(x)的最小值;
,研究F(x)的最小值;

 星级口算天天练系列答案
星级口算天天练系列答案