
 现不放回从袋中摸取球,每次摸一球,直到取到白球时即终止,每个球在每一次被取出的机会是等可能的,用
现不放回从袋中摸取球,每次摸一球,直到取到白球时即终止,每个球在每一次被取出的机会是等可能的,用 表示取球终止时所需要的取球次数.
表示取球终止时所需要的取球次数. 的分布列和数学期望.
的分布列和数学期望.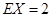 .
.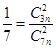 ,利用组合数的计算,计算出n的值,从而得到白球和黑球个数;第二问,利用第一问的结论,利用不放回抽样,计算出每一种情况的概率,列出分布列,利用
,利用组合数的计算,计算出n的值,从而得到白球和黑球个数;第二问,利用第一问的结论,利用不放回抽样,计算出每一种情况的概率,列出分布列,利用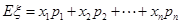 计算出数学期望.
计算出数学期望.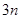 个白球,则有
个白球,则有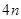 个黑球.
个黑球.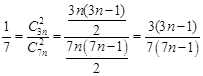 , 4分
, 4分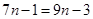 ,解得
,解得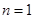 ,
, 的取值是
的取值是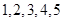 .
.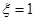 ,即第1次取到白球,
,即第1次取到白球,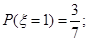
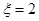 ,即第2次取到白球
,即第2次取到白球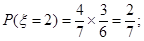
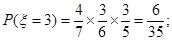
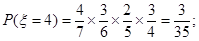
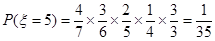 10分
10分 分布列为
分布列为 | 1 | 2 | 3 | 4 | 5 |
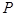 | 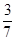 | 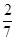 | 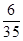 | 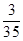 | 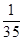 |
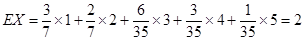 12分
12分

科目:高中数学 来源:不详 题型:解答题
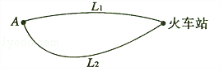
| 所用时间(分钟) | 10~20 | 20~30 | 30~40 | 40~50 | 50~60 |
| 选择L1的人数 | 6 | 12 | 18 | 12 | 12 |
| 选择L2的人数 | 0 | 4 | 16 | 16 | 4 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
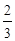 ,中奖可以获得2分;方案乙的中奖率为
,中奖可以获得2分;方案乙的中奖率为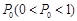 ,中奖可以获得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,晚会结束后凭分数兑换奖品.
,中奖可以获得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,晚会结束后凭分数兑换奖品.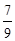 ,求
,求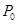 ;
;查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 .据以往资料统计,第一场比赛组织者可获得门票收入40万元,以后每场比赛门票收入比上一场增加10万元,则组织者在此次决赛中要获得的门票收入不少于390万元的概率为________.
.据以往资料统计,第一场比赛组织者可获得门票收入40万元,以后每场比赛门票收入比上一场增加10万元,则组织者在此次决赛中要获得的门票收入不少于390万元的概率为________.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
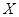 为选出的3名同学中女同学的人数,求随机变量
为选出的3名同学中女同学的人数,求随机变量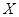 的分布列和数学期望.
的分布列和数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A.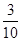 | B.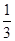 | C.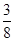 | D.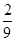 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com