
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| π |
| 4 |
| π |
| 3 |
| D1E |
查看答案和解析>>
科目:高中数学 来源: 题型:
| D1E |
查看答案和解析>>
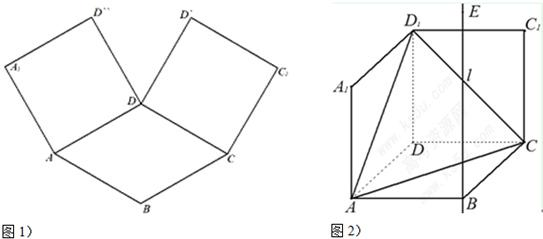
科目:高中数学 来源:2011届甘肃省河西五市高三第二次联考理科数学文卷 题型:解答题
(本小题满分12分)
如图1,在平面内,ABCD边长为2的正方形,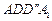 和
和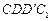 都是正方形。将两个正方形分别沿AD,CD折
都是正方形。将两个正方形分别沿AD,CD折 起,使
起,使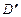 与
与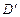 重合于点D1。设直线l过点B且垂直于正方形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面A
重合于点D1。设直线l过点B且垂直于正方形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面A BCD同侧,设
BCD同侧,设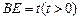 (图2)。
(图2)。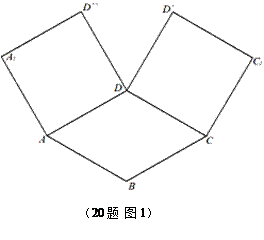
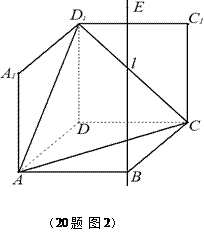
(1)设二面角E – AC – D1的大小为q,当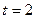 时,求
时,求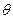 的余弦值;
的余弦值;
(2)当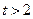 时在线段
时在线段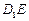 上是否存在点
上是否存在点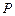 ,使平面
,使平面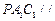 平面
平面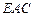 ,若存在,求出
,若存在,求出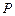 分
分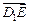 所成的比
所成的比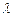 ;若不存在,请说明理由。
;若不存在,请说明理由。
查看答案和解析>>
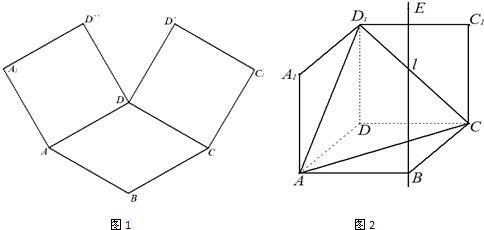
科目:高中数学 来源:2010-2010-2011学年四川省高三四月月考文科数学卷 题型:解答题
如图1,在平面内,ABCD是 且
且 的菱形,
的菱形, 和
和 都是正方形。将两个正方形分别沿AD,CD折起,使
都是正方形。将两个正方形分别沿AD,CD折起,使 与
与 重合于点D1。设直线l过点B且垂直于菱形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面ABCD同侧,设
重合于点D1。设直线l过点B且垂直于菱形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面ABCD同侧,设 (图2)。
(图2)。


(1)设二面角E – AC – D1的大小为q ,若 ,求
,求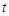 的取值范围;
的取值范围;
(2)在线段 上是否存在点
上是否存在点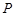 ,使平面
,使平面 平面
平面 ,若存在,求出
,若存在,求出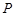 分
分 所成的比
所成的比 ;若不存在,请说明理由。
;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源:2012届福建省高二下学期期末考试数学(理) 题型:填空题
2002年8月在北京召开的国际数学家大会会标如右图所示,它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形.如果在5个区域内用红、橙、黄、绿四种颜色进行涂色,要求相邻区域不能同色,则涂色的方案有_____种.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com