
(12分) 如图7-4,已知△ABC中, ∠ACB=90°,CD⊥AB,且AD=1,BD=2,△ACD绕CD旋转至A′CD,使点A′与点B之间的距离A′B=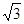 。
。
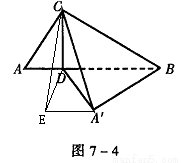
(1)求证:BA′⊥平面A′CD;
(2)求二面角A′-CD-B的大小;
(3)求异面直线A′C与BD所成的角的余弦值。
解 (1)∵CD⊥AB,
∴CD⊥A′D,CD⊥DB,
∴CD⊥平面A′BD,
∴CD⊥BA′。
又在△A′DB中,A′D=1,DB=2,A′B=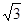 ,
,
∴∠BA′D=90°,即BA′⊥A′D,
∴BA′⊥平面A′CD。
(2)∵CD⊥DB,CD⊥A′D,
∴∠BDA′是二面角A′—CD—B的平面角。
又Rt△A′BD中,A′D=1,BD=2,
∴∠A′DB=60°,
即 二面角A′—CD—B为60°。
(3)过A′作A′E∥BD,在平面A′BD中作DE⊥A′E于E,连CE,则∠CA′E为A′C与BD所成角。
∵CD⊥平面A′BD,DE⊥A′E,∴A′E⊥CE。
∵EA′∥AB,∠A′DB=60°,∴∠DA′E=60°,
又A′D=1,∠DEA′=90°,
∴A′E=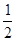
又∵在Rt△ACB中,AC=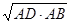 =
=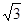
∴A′C=AC=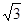
∴Rt△CEA′中,cos∠CA′E=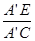 =
=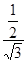 =
=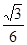 ,
,
即异面直线A′C与BD所成角的余弦值为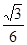 。
。
【解析】略


 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:高中数学 来源:2014届河南灵宝第三高级中学高二上学期第二次质量检测文数(解析版) 题型:解答题
(本小题满分12分)
如图,在四边形ABCD中,AC平分∠DAB,∠ABC=600,AC=7,AD=6,S△ADC=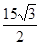 ,
,
求AB的长.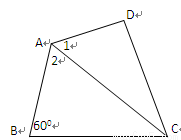
查看答案和解析>>
科目:高中数学 来源:2011-2012学年重庆市高三下学期第一次月考理科数学 题型:解答题
(本小题满分12分,(1)小问5分,(2)小分7分.)
如图所示,正三棱柱 的底面边长与侧棱长均为
的底面边长与侧棱长均为 ,
, 为
为 中点.
中点.
(1)求证: ∥平面
∥平面 ;
;
(2)求直线 与平面
与平面 所成的角的正弦值.
所成的角的正弦值.

查看答案和解析>>
科目:高中数学 来源:2011-2012学年上海市嘉定区高三年级第一次质量调研理科数学 题型:解答题
(本题满分12分)本题共有2个小题,第1小题满分5分,第2小题满分7分.
如图,在直三棱柱 中,
中,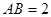 ,
, ,
, .
.
(1)求三棱柱 的表面积
的表面积 ;
;
(2)求异面直线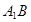 与
与 所成角的大小(结果用反三角函数表示).
所成角的大小(结果用反三角函数表示).

查看答案和解析>>
科目:高中数学 来源:2010-2011年河南省郑州市高二下学期第一次月考数学文卷 题型:解答题
(本小题满分12分)
如图所示茎叶图是青年歌手电视大奖赛中7位评委给参加最后决赛的两位选手甲、乙评定的成绩,程序框图用来编写程序统计每位选手的成绩(各评委所给有效分数的平均值),试根据下面条件回答下列问题:
1)根据茎叶图,乙选手的成绩中,中位数是 ,众数是 。
2)在程序框图中,用k表示评委人数,用a表示选手的最后成绩(各评委所给有效分数的平均值)那么图中①②处分别为 , 。“S1=S-max-min”的含义
” 。
3) 根据程序框图,甲的最后成绩是 ;乙的最后成绩是 。

查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分13分)
如图7所示,在边长为12的正方形![]() 中,
中,![]() ,且AB=3,BC=4,
,且AB=3,BC=4,![]() 分别交BB1,CC1于点P、Q,将该正方形沿BB1、CC1折叠,使得
分别交BB1,CC1于点P、Q,将该正方形沿BB1、CC1折叠,使得![]() 与AA1重合,构成如图5所示的三棱柱ABC—A1B1C1,请在图5中解决下列问题:
与AA1重合,构成如图5所示的三棱柱ABC—A1B1C1,请在图5中解决下列问题:
(1)求证:![]() ;
;
(2)在底边AC上有一点M,满足AM:MC=3:4,求证:BM//平面APQ。
(3)求直线BC与平面APQ所成角的正弦值。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com