
已知函数f(x)=ax2+ln(x+1).
(1)当a=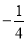 时,求函数f(x)的单调区间;
时,求函数f(x)的单调区间;
(2)当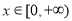 时,函数y=f(x)图像上的点都在
时,函数y=f(x)图像上的点都在 所表示的平面区域内,求实数a的取值范围;
所表示的平面区域内,求实数a的取值范围;
(3)求证: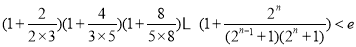 (其中
(其中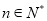 ,e是自然数对数的底数)
,e是自然数对数的底数)
(1)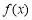 的单调递增区间为
的单调递增区间为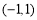 ,单调递减区间为
,单调递减区间为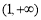 (2)
(2) (3)见解析
(3)见解析
【解析】
试题分析:
(1)函数f(x)是二次与对数的结合,求单调性可以利用导数,以此先求定义域,求导,求导函数大于0与小于0分别求出单调递增与单调递减区间.
(2)要使得函数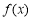 图象上的点都在
图象上的点都在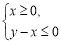 所表示的平面区域内,则当
所表示的平面区域内,则当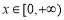 时,
时,
不等式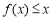 恒成立即可,即转化了恒成立问题,则只需要
恒成立即可,即转化了恒成立问题,则只需要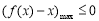 ,故考虑对
,故考虑对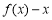 求导求单调性来确定函数在
求导求单调性来确定函数在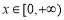 上的最大值,因为导函数含有参数a,所以在求解单调性确定最值的过程中需要讨论a的范围,讨论需从两根的大小和0的大小进行分析才能确定
上的最大值,因为导函数含有参数a,所以在求解单调性确定最值的过程中需要讨论a的范围,讨论需从两根的大小和0的大小进行分析才能确定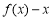 的最值,从而得到a的取值范围.
的最值,从而得到a的取值范围.
(3)考虑把不等式两边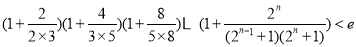 同时去对数再证明,即证明
同时去对数再证明,即证明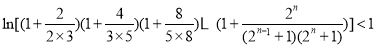 ,利用对数的乘法公式可以把不等式的左边化解成为不可求和数列的和,在利用利用(2)得到当a=0时,ln(1+x)
,利用对数的乘法公式可以把不等式的左边化解成为不可求和数列的和,在利用利用(2)得到当a=0时,ln(1+x)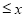 是恒成立的,把不可求和数列放缩成为可以裂项求和的数列,裂项利用
是恒成立的,把不可求和数列放缩成为可以裂项求和的数列,裂项利用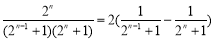 ,进而证明原不等式.
,进而证明原不等式.
试题解析:
(1)当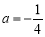 时,
时,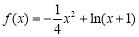 (
(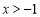 ),
),
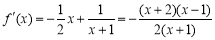 (
(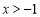 ), 1分
), 1分
由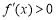 解得
解得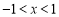 ,由
,由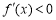 解得
解得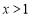 .
.
故函数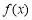 的单调递增区间为
的单调递增区间为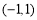 ,单调递减区间为
,单调递减区间为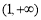 . 3分
. 3分
(2)因函数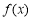 图象上的点都在
图象上的点都在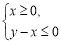 所表示的平面区域内,则当
所表示的平面区域内,则当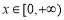 时,
时,
不等式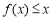 恒成立,即
恒成立,即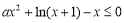 恒成立,
恒成立,
设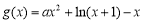 (
(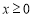 ),只需
),只需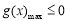 即可. 4分
即可. 4分
由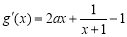
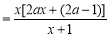 ,
,
(ⅰ)当 时,
时,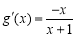 ,当
,当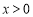 时,
时,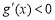 ,
,
函数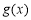 在
在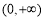 上单调递减,故
上单调递减,故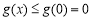 成立. 5分
成立. 5分
(ⅱ)当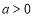 时,由
时,由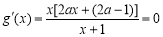 ,因
,因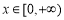 ,所以
,所以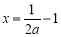 ,
,
①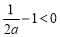 ,即
,即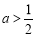 时,在区间
时,在区间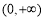 上,
上,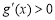 ,则函数
,则函数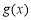 在
在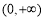 上单调递增,
上单调递增,
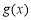 在
在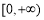 上无最大值(或:当
上无最大值(或:当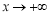 时,
时,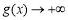 ),此时不满足条件;
),此时不满足条件;
②若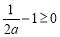 ,即
,即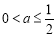 时,函数
时,函数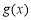 在
在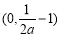 上单调递减,
上单调递减,
在区间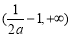 上单调递增,同样
上单调递增,同样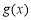 在
在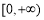 上无最大值,不满足条件. 8分
上无最大值,不满足条件. 8分
(ⅲ)当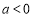 时,由
时,由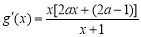 ,∵
,∵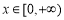 ,∴
,∴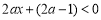 ,
,
∴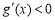 ,故函数
,故函数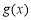 在
在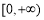 上单调递减,故
上单调递减,故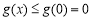 成立.
成立.
综上所述,实数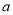 的取值范围是
的取值范围是 . 10分
. 10分
(3)据(2)知当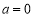 时,
时,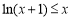 在
在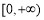 上恒成立.
上恒成立.
(或另证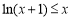 在区间
在区间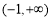 上恒成立), 11分
上恒成立), 11分
又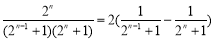 ,
,
∵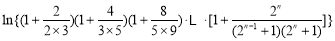
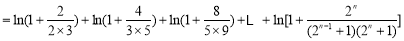
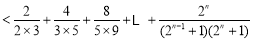

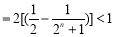 ,
,

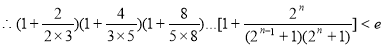 . 14分
. 14分
考点:导数单调性恒成立数形结合不等式


科目:高中数学 来源:2013-2014学年广东省肇庆市高三3月第一次模拟文科数学试卷(解析版) 题型:选择题
已知圆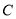 的圆心是直线
的圆心是直线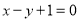 与
与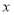 轴的交点,且圆
轴的交点,且圆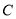 与直线
与直线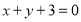 相切,则圆
相切,则圆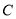 的方程是( )
的方程是( )
A.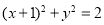 B.
B.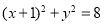
C.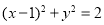 D.
D.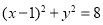
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省湛江市高三高考模拟测试二文科数学试卷(解析版) 题型:选择题
下列命题正确的是( )
A.若两条直线和同一个平面所成的角相等,则这两条直线平行
B.若一个平面内有三个点到另一个平面的距离相等,则这两个平面平行
C.若一条直线平行于两个相交平面,则这条直线与这两个平面的交线平行
D.若两个平面都垂直于第三个平面,则这两个平面平行
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省梅州市高三3月总复习质检理科数学试卷(解析版) 题型:解答题
已知函数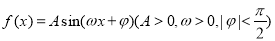 的部分图像如图所示.
的部分图像如图所示.
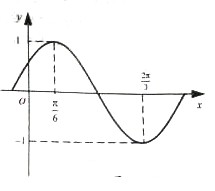
(1)求函数f(x)的解析式,并写出f(x)的单调减区间;
(2)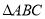 的内角分别是A,B,C.若f(A)=1,
的内角分别是A,B,C.若f(A)=1,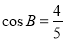 ,求sinC的值.
,求sinC的值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省梅州市高三3月总复习质检文科数学试卷(解析版) 题型:填空题
已知双曲线C的焦点、实轴端点恰好是椭圆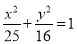 的长轴的端点、焦点,则双曲线C的方程为_______.
的长轴的端点、焦点,则双曲线C的方程为_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com