
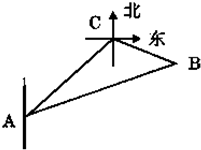
 一缉私艇在A处发现在北偏东45°方向距离12海里的海面上C处有一走私船正以10海里/小时的速度沿东偏南15°方向逃窜,缉私艇的速度为14海里/小时.若要在最短的时间内追上该走私船,缉私艇应沿北偏东45°+α的方向去追,求追及所需时间和α角的正弦值.
一缉私艇在A处发现在北偏东45°方向距离12海里的海面上C处有一走私船正以10海里/小时的速度沿东偏南15°方向逃窜,缉私艇的速度为14海里/小时.若要在最短的时间内追上该走私船,缉私艇应沿北偏东45°+α的方向去追,求追及所需时间和α角的正弦值.| AB |
| sin∠ACB |
| BC |
| sin∠BAC |
| AB |
| sin∠ACB |
| BC |
| sin∠BAC |
| 20sin120° |
| 28 |
5
| ||
| 14 |
5
| ||
| 14 |


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:高中数学 来源:北京市日坛中学2010-2011学年高一下学期期中试题数学试题 题型:044
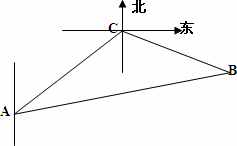
一缉私艇在A处发现在北偏东45°方向,距离12n mile的海面C处有一走私船正以10n mile/h的速度沿东偏南15°方向逃窜,缉私艇的速度为14n mile/h,若要在最短的时间内追上该走私船,缉私艇应沿北偏东45°+α的方向去追,求追击所需的时间和α角的正弦值.
查看答案和解析>>
科目:高中数学 来源:山西省山大附中2011-2012学年高一5月月考数学试题(B) 题型:044
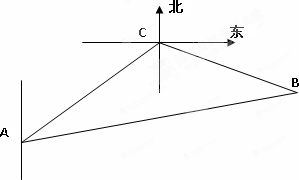
一缉私艇在A处发现在其北偏东45°方向,距离12 nmile的海面C处有一走私船正以10 nmile/h的速度沿东偏南15°方向逃窜.缉私艇的速度为14 nmile/h,若要在最短的时间内追上该走私船,缉私艇应沿北偏东45°+α的方向去追,求追及所需的时间和α角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图所示:一缉私艇在A处发现在北偏东![]() 方向,距离12 海里的海面上C处有一走私船正以10 海里/小时的速度沿东偏南
方向,距离12 海里的海面上C处有一走私船正以10 海里/小时的速度沿东偏南![]() 方向逃窜.缉私艇的速度为14 海里/小时. 若要在最短的时间内追上该走私船,缉私艇应沿北偏东
方向逃窜.缉私艇的速度为14 海里/小时. 若要在最短的时间内追上该走私船,缉私艇应沿北偏东![]() 的方向去追,.求追及所需的时间和
的方向去追,.求追及所需的时间和![]() 角的正弦值。
角的正弦值。
查看答案和解析>>
科目:高中数学 来源:2011--2012学年山西省高一5月月考数学试卷(解析版) 题型:解答题
(本小题共12分)
一缉私艇在A处发现在其北偏东 方向,距离12 nmile的海面C处有一走私船正以10 nmile/h的速度沿东偏南
方向,距离12 nmile的海面C处有一走私船正以10 nmile/h的速度沿东偏南 方向逃窜.缉私艇的速度为14 nmile/h, 若要在最短的时间内追上该走私船,缉私艇应沿北偏东
方向逃窜.缉私艇的速度为14 nmile/h, 若要在最短的时间内追上该走私船,缉私艇应沿北偏东 的方向去追,求追及所需的时间和
的方向去追,求追及所需的时间和 角的正弦值.
角的正弦值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com