
科目: 来源:0101 期中题 题型:单选题
[ ]
查看答案和解析>>
科目: 来源:0101 期中题 题型:解答题
 是奇函数,
是奇函数,查看答案和解析>>
科目: 来源:0103 期中题 题型:单选题
[ ]
 )
) 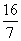 )
) 查看答案和解析>>
科目: 来源:0103 期中题 题型:解答题
 ,x∈(0,+∞)的性质。列表如下:
,x∈(0,+∞)的性质。列表如下: 
请观察表中y值随x值变化的特点,完成以下的问题。
(1)函数f(x)=x+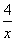 ,x∈(0,+∞)在区间(0,2)上递减;在区间_____上递增。当x=_____时,y最小=_____。
,x∈(0,+∞)在区间(0,2)上递减;在区间_____上递增。当x=_____时,y最小=_____。
(2)证明:函数f(x)=x+ (x>0)在区间(0,2)递减;
(x>0)在区间(0,2)递减;
(3)思考:函数f(x)=x+ (x<0)有最值吗?如有,是最大值还是最小值?此时x为何值?(直接回答结果,不需证明)。
(x<0)有最值吗?如有,是最大值还是最小值?此时x为何值?(直接回答结果,不需证明)。
查看答案和解析>>
科目: 来源:0115 期末题 题型:单选题
查看答案和解析>>
科目: 来源:广东省模拟题 题型:解答题
已知函数f(x)=ax2+bx+c(a≠0)满足f(0)=0,对于任意x∈R都有f(x)≥x,且f( +x)=f(
+x)=f( -x),令g(x)=f(x)-|λx-1|(λ>0)。
-x),令g(x)=f(x)-|λx-1|(λ>0)。
(1)求函数f(x)的表达式;
(2)求函数g(x)的单调区间;
(3)研究函数g(x)在区间(0,1)上的零点个数。
查看答案和解析>>
科目: 来源:0103 期中题 题型:解答题
查看答案和解析>>
科目: 来源:0103 期中题 题型:解答题
 ,且f(1)=2,
,且f(1)=2,查看答案和解析>>
科目: 来源:0103 期中题 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com