
科目: 来源:2017届吉林省吉林市高三毕业班第二次调研测试数学(理)试卷(解析版) 题型:填空题
已知 是坐标原点,点
是坐标原点,点 ,若点
,若点 为平面区域
为平面区域 上一个动点,则
上一个动点,则 的取值范围是__________.
的取值范围是__________.
查看答案和解析>>
科目: 来源:2017届吉林省吉林市高三毕业班第二次调研测试数学(理)试卷(解析版) 题型:填空题
艾萨克·牛顿(1643年1月4日----1727年3月31日)英国皇家学会会长,英国著名物理学家,同时在数学上也有许多杰出贡献,牛顿用“作切线”的方法求函数 零点时给出一个数列
零点时给出一个数列 :满足
:满足 ,我们把该数列称为牛顿数列。
,我们把该数列称为牛顿数列。
如果函数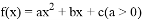 有两个零点1,2,数列
有两个零点1,2,数列 为牛顿数列,设
为牛顿数列,设 ,已知
,已知 ,
, ,则
,则 的通项公式
的通项公式 __________.
__________.
查看答案和解析>>
科目: 来源:2017届吉林省吉林市高三毕业班第二次调研测试数学(理)试卷(解析版) 题型:解答题
已知函数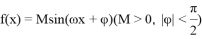 的部分图象如图所示.
的部分图象如图所示.

(1)求函数 的解析式;
的解析式;
(2)在 中,角
中,角 的对边分别是
的对边分别是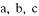 ,若
,若 ,求
,求 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源:2017届吉林省吉林市高三毕业班第二次调研测试数学(理)试卷(解析版) 题型:解答题
已知数列 是等比数列,
是等比数列, 为数列
为数列 的前
的前 项和,且
项和,且 ,
, .
.
(1)求数列 的通项公式;
的通项公式;
(2)设 ,且
,且 为递增数列,若
为递增数列,若 ,求证:
,求证: .
.
查看答案和解析>>
科目: 来源:2017届吉林省吉林市高三毕业班第二次调研测试数学(理)试卷(解析版) 题型:解答题
某车间20名工人年龄数据如下表:
年龄(岁) | 19 | 24 | 26 | 30 | 34 | 35 | 40 | 合计 |
工人数(人) | 1 | 3 | 3 | 5 | 4 | 3 | 1 | 20 |
(1)求这20名工人年龄的众数与平均数;
(2)以十位数为茎,个位数为叶,作出这20名工人年龄的茎叶图;
(3)从年龄在24和26的工人中随机抽取2人,求这2人均是24岁的概率.
查看答案和解析>>
科目: 来源:2017届吉林省吉林市高三毕业班第二次调研测试数学(理)试卷(解析版) 题型:解答题
如图,在四棱锥 中,底面
中,底面 是菱形,且
是菱形,且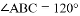 ,点
,点 是棱
是棱 的中点,平面
的中点,平面 与棱
与棱 交于点
交于点 .
.

(1)求证: ;
;
(2)若 ,平面
,平面 平面
平面 ,求平面
,求平面 与平面
与平面 所成的二面角的余弦值.
所成的二面角的余弦值.
查看答案和解析>>
科目: 来源:2017届吉林省吉林市高三毕业班第二次调研测试数学(理)试卷(解析版) 题型:解答题
如图,椭圆 ,点
,点 在短轴
在短轴 上,且
上,且 .
.

(1)求椭圆 的方程及离心率;
的方程及离心率;
(2)设 为坐标原点,过点
为坐标原点,过点 的动直线与椭圆交于
的动直线与椭圆交于 ,
, 两点,是否存在常数
两点,是否存在常数 ,使得
,使得 为定值?若存在,求
为定值?若存在,求 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源:2017届吉林省吉林市高三毕业班第二次调研测试数学(理)试卷(解析版) 题型:解答题
设函数 ,
, ,已知曲线
,已知曲线 在点
在点 处的切线与直线
处的切线与直线 垂直.
垂直.
(1)求 的值;
的值;
(2)若对任意 ,都有
,都有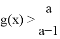 ,求
,求 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com