
科目: 来源: 题型:
【题目】平面直角坐标系![]() 中,过椭圆
中,过椭圆![]() :
: ![]() (
(![]() )焦点的直线
)焦点的直线![]() 交
交![]() 于
于![]() 两点,
两点, ![]() 为
为![]() 的中点,且
的中点,且![]() 的斜率为9.
的斜率为9.
(Ⅰ)求![]() 的方程;
的方程;
(Ⅱ)![]() 是
是![]() 的左、右顶点,
的左、右顶点, ![]() 是
是![]() 上的两点,若
上的两点,若![]() ,求四边形
,求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,四棱锥P﹣ABCD的底面ABCD是边长为1的菱形,∠BCD=60°,E是CD的中点,PA⊥底面ABCD,PA=![]() .
.
(Ⅰ)证明:平面PBE⊥平面PAB;
(Ⅱ)求二面角A﹣BE﹣P的大小.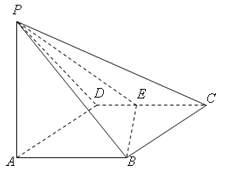
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示的几何体中,四边形ABCD是矩形,平面ABCD⊥平面ABE,已知AB=2,AE=BE= ![]() ,且当规定正视图方向垂直平面ABCD时,该几何体的侧视图的面积为
,且当规定正视图方向垂直平面ABCD时,该几何体的侧视图的面积为 ![]() .若M,N分别是线段DE、CE上的动点,则AM+MN+NB的最小值为
.若M,N分别是线段DE、CE上的动点,则AM+MN+NB的最小值为 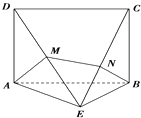
查看答案和解析>>
科目: 来源: 题型:
【题目】平面α过正方体ABCD﹣A1B1C1D1的顶点A,α∥平面CB1D1 , α∩平面ABCD=m,α∩平面AB B1A1=n,则m,n所成角的正弦值为 .
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.
(1)求PB和平面PAD所成的角的大小;
(2)证明AE⊥平面PCD.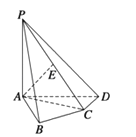
查看答案和解析>>
科目: 来源: 题型:
【题目】正方体ABCD﹣A1B1C1D1中,点M,N分别在线段AB1、BC1上,且AM=BN.以下结论:①AA1⊥MN;②A1C1∥MN;③MN∥平面A1B1C1D1;④MN与A1C1异面,⑤MN与 A1C1成30°.其中有可能成立的结论的个数为( ) 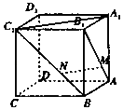
A.5
B.4
C.3
D.2
查看答案和解析>>
科目: 来源: 题型:
【题目】某理财公司有两种理财产品![]() 和
和![]() .这两种理财产品一年后盈亏的情况如下(每种理财产品的不同投资结果之间相互独立):
.这两种理财产品一年后盈亏的情况如下(每种理财产品的不同投资结果之间相互独立):
产品![]()
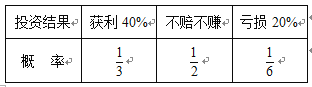
产品![]() (其中
(其中![]() )
)
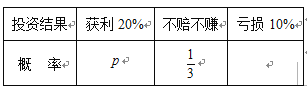
(Ⅰ)已知甲、乙两人分别选择了产品![]() 和产品
和产品![]() 进行投资,如果一年后他们中至少有一人获利的概率大于
进行投资,如果一年后他们中至少有一人获利的概率大于![]() ,求
,求![]() 的取值范围;
的取值范围;
(Ⅱ)丙要将家中闲置的10万元钱进行投资,以一年后投资收益的期望值为决策依据,在产品![]() 和产品
和产品![]() 之中选其一,应选用哪个?
之中选其一,应选用哪个?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在底面为平行四边形的四棱锥P﹣ABCD中,AB⊥AC,PA⊥平面ABCD,且PA=AB,点E是PD的中点.
(Ⅰ)求证:AC⊥PB;
(Ⅱ)求证:PB∥平面AEC.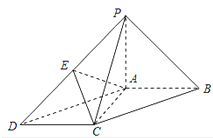
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com