
科目: 来源: 题型:
【题目】已知动圆C过点(1,0),且于直线x=﹣1相切.
(1)求圆心C的轨迹M的方程;
(2)A,B是M上的动点,O是坐标原点,且![]()
![]()
![]() , 求证:直线AB过定点,并求出该点坐标.
, 求证:直线AB过定点,并求出该点坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在棱长为1的正方体ABCD﹣A1B1C1D1中,点E是棱AB上的动点.
(1)求证:DA1⊥ED1;
(2)若直线DA1与平面CED1成角为45°,求![]() 的值.
的值.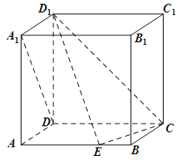
查看答案和解析>>
科目: 来源: 题型:
【题目】【南京市、盐城市2017届高三年级第二次模拟】(本小题满分14分)
在一张足够大的纸板上截取一个面积为3600平方厘米的矩形纸板ABCD,然后在矩形纸板的四个角上切去边长相等的小正方形,再把它的边沿虚线折起,做成一个无盖的长方体纸盒(如图).设小正方形边长为x厘米,矩形纸板的两边AB,BC的长分别为a厘米和b厘米,其中a≥b.
(1)当a=90时,求纸盒侧面积的最大值;
(2)试确定a,b,x的值,使得纸盒的体积最大,并求出最大值.

查看答案和解析>>
科目: 来源: 题型:
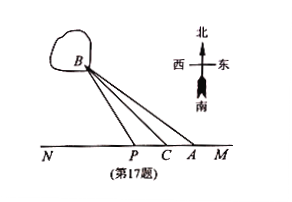
【题目】【苏北四市2016-2017学年度高三年级第一学期期末调研】如图,已知![]() 两镇分别位于东西湖岸
两镇分别位于东西湖岸![]() 的
的![]() 处和湖中小岛的
处和湖中小岛的![]() 处,点
处,点![]() 在
在![]() 的
的
正西方向![]() 处,
处,![]() .现计划铺设一条电缆联通
.现计划铺设一条电缆联通![]() 两镇,有
两镇,有
两种铺设方案:①沿线段![]() 在水下铺设;②在湖岸
在水下铺设;②在湖岸![]() 上选一点
上选一点![]() ,先沿线段
,先沿线段![]() 在地
在地
下铺设,再沿线段![]() 在水下铺设,预算地下、水下的电缆铺设费用分别为
在水下铺设,预算地下、水下的电缆铺设费用分别为![]() 万元∕
万元∕![]() 、
、
![]() 万元∕
万元∕![]() .
.
(1)求![]() 两镇间的距离;
两镇间的距离;
(2)应该如何铺设,使总铺设费用最低?
查看答案和解析>>
科目: 来源: 题型:
【题目】2012年“双节”期间,高速公路车辆较多.某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(km/t)分成六段:(60,65),[65,70),[70,75),[80,85),[85,90)后得到如图的频率分布直方图.
(1)某调查公司在采样中,用到的是什么抽样方法?
(2)求这40辆小型车辆车速的众数和中位数的估计值.
(3)若从车速在[60,70)的车辆中任抽取2辆,求车速在[65,70)的车辆至少有一辆的概率.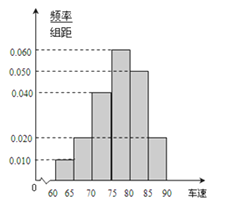
查看答案和解析>>
科目: 来源: 题型:
【题目】已知矩形ABCD,AB=1,BC=![]() . 将△ABD沿矩形的对角线BD所在的直线进行翻折,在翻折过程中( )
. 将△ABD沿矩形的对角线BD所在的直线进行翻折,在翻折过程中( )
A.存在某个位置,使得直线AC与直线BD垂直
B.存在某个位置,使得直线AB与直线CD垂直
C.存在某个位置,使得直线AD与直线BC垂直
D.对任意位置,三对直线“AC与BD”,“AB与CD”,“AD与BC”均不垂直
查看答案和解析>>
科目: 来源: 题型:
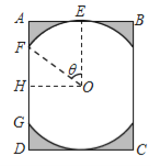
【题目】【苏北三市(连云港、徐州、宿迁)2017届高三年级第三次调研考试】某景区修建一栋复古建筑,其窗户设计如图所示.圆![]() 的圆心与矩形
的圆心与矩形![]() 对角线的交点重合,且圆与矩形上下两边相切(
对角线的交点重合,且圆与矩形上下两边相切(![]() 为上切点),与左右两边相交(
为上切点),与左右两边相交(![]() ,
,![]() 为其中两个交点),图中阴影部分为不透光区域,其余部分为透光区域.已知圆的半径为1
为其中两个交点),图中阴影部分为不透光区域,其余部分为透光区域.已知圆的半径为1![]() ,且
,且![]() ,设
,设![]() ,透光区域的面积为
,透光区域的面积为![]() .
.
(1)求![]() 关于
关于![]() 的函数关系式,并求出定义域;
的函数关系式,并求出定义域;
(2)根据设计要求,透光区域与矩形窗面的面积比值越大越好.当该比值最大时,求边![]() 的长度.
的长度.
查看答案和解析>>
科目: 来源: 题型:
【题目】【2016-2017学年度苏锡常镇四市高三教学情况调研(二)】某科研小组研究发现:一棵水蜜桃树的产量![]() (单位:百千克)与肥料费用
(单位:百千克)与肥料费用![]() (单位:百元)满足如下关系:
(单位:百元)满足如下关系:![]() ,且投入的肥料费用不超过5百元.此外,还需要投入其他成本(如施肥的人工费等)
,且投入的肥料费用不超过5百元.此外,还需要投入其他成本(如施肥的人工费等)![]() 百元.已知这种水蜜桃的市场售价为16元/千克(即16百元/百千克),且市场需求始终供不应求.记该棵水蜜桃树获得的利润为
百元.已知这种水蜜桃的市场售价为16元/千克(即16百元/百千克),且市场需求始终供不应求.记该棵水蜜桃树获得的利润为![]() (单位:百元).
(单位:百元).
(1)求利润函数![]() 的函数关系式,并写出定义域;
的函数关系式,并写出定义域;
(2)当投入的肥料费用为多少时,该水蜜桃树获得的利润最大?最大利润是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】下列四个命题:
①样本方差反映的是所有样本数据与样本平均值的偏离程度;
②某校高三一级部和二级部的人数分别是m、n,本次期末考试两级部数学平均分分别是a、b,则这两个级部的数学平均分为 ![]() +
+ ![]() ;
;
③某中学采用系统抽样方法,从该校高一年级全体800名学生中抽50名学生做牙齿健康检查,现将800名学生从001到800进行编号,已知从497﹣﹣512这16个数中取得的学生编号是503,则初始在第1小组00l~016中随机抽到的学生编号是007.
其中命题正确的个数是( )
A.0个
B.1个
C.2个
D.3个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com