
【题目】2012年“双节”期间,高速公路车辆较多.某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(km/t)分成六段:(60,65),[65,70),[70,75),[80,85),[85,90)后得到如图的频率分布直方图.
(1)某调查公司在采样中,用到的是什么抽样方法?
(2)求这40辆小型车辆车速的众数和中位数的估计值.
(3)若从车速在[60,70)的车辆中任抽取2辆,求车速在[65,70)的车辆至少有一辆的概率.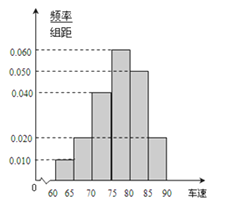
【答案】解:(1)由题意知这个抽样是按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,是一个具有相同间隔的抽样,并且总体的个数比较多,这是一个系统抽样.
故调查公司在采样中,用到的是系统抽样,
(2)众数的估计值为最高的矩形的中点,即众数的估计值等于77.5
设图中虚线所对应的车速为x,则中位数的估计值为:
0.01×5+0.02×5+0.04×5+0.06×(x﹣75)=0.5,
解得x=77.5,即中位数的估计值为77.5
(3)从图中可知,车速在[60,65)的车辆数为:m1=0.01×5×40=2(辆),
车速在[65,70)的车辆数为:m2=0.02×5×40=4(辆)
设车速在[60,65)的车辆设为a,b,车速在[65,70)的车辆设为c,d,e,f,
则所有基本事件有:(a,b),(a,c),(a,d),(a,e),(a,f),(b,c),(b,d),(b,e),(b,f),(c,d),(c,e),(c,f),(d,e),(d,f),(e,f)共15种 (10分)
其中车速在[65,70)的车辆至少有一辆的事件有:(a,c),(a,d),(a,e),(a,f),(b,c),(b,d),(b,e),(b,f),(c,d),(c,e),(c,f),(d,e),(d,f),(e,f)共14种
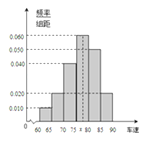
所以,车速在[65,70)的车辆至少有一辆的概率为P=![]() .
.
【解析】(1)这个抽样是按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,是一个具有相同间隔的抽样,并且总体的个数比较多,这是一个系统抽样;
(2)选出直方图中最高的矩形求出其底边的中点即为众数;求出从左边开始小矩形的面积和为0.5对应的横轴的左边即为中位数;利用各个小矩形的面积乘以对应矩形的底边的中点的和为数据的平均数.
(3)从图中可知,车速在[60,65)的车辆数和车速在[65,70)的车辆数.从车速在(60,70)的车辆中任抽取2辆,设车速在[60,65)的车辆设为a,b,车速在[65,70)的车辆设为c,d,e,f,列出各自的基本事件数,从而求出相应的概率即可.
【考点精析】根据题目的已知条件,利用用样本的频率分布估计总体分布的相关知识可以得到问题的答案,需要掌握样本数据的频率分布表和频率分布直方图,是通过各小组数据在样本容量中所占比例大小来表示数据的分布规律,它可以让我们更清楚的看到整个样本数据的频率分布情况,并由此估计总体的分布情况.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:
【题目】已知数列{an}满足 ![]() ,
, ![]() ,n∈N* .
,n∈N* .
(1)求证:数列 ![]() 为等比数列;
为等比数列;
(2)是否存在互不相等的正整数m,s,t,使m,s,t成等差数列,且am﹣1,as﹣1,at﹣1成等比数列?如果存在,求出所有符合条件的m,s,t;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【苏北四市2016-2017学年度高三年级第一学期期末调研】如图,在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的离心率为
的离心率为![]() ,且右焦点
,且右焦点![]() 到左准线的距离为
到左准线的距离为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设![]() 为椭圆
为椭圆![]() 的左顶点,
的左顶点,![]() 为椭圆
为椭圆![]() 上位于
上位于![]() 轴上方的点,直线
轴上方的点,直线![]() 交
交![]() 轴于点
轴于点
![]() ,过点
,过点![]() 作
作![]() 的垂线,交
的垂线,交![]() 轴于点
轴于点![]() .
.
(ⅰ)当直线的![]() 斜率为
斜率为![]() 时,求
时,求![]() 的外接圆的方程;
的外接圆的方程;
(ⅱ)设直线![]() 交椭圆
交椭圆![]() 于另一点
于另一点![]() ,求
,求![]() 的面积的最大值.
的面积的最大值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}是首项为a1 , 公比为q的等比数列,Sn是{an}的前n项和.Sn= ![]() ;若am+an=as+at , 则m+n=s+t;Sk , S2k﹣Sk , S3k﹣S2k成等比数列(k∈N).
;若am+an=as+at , 则m+n=s+t;Sk , S2k﹣Sk , S3k﹣S2k成等比数列(k∈N).
以上说法正确的有( )个.
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设an= ![]() sin
sin ![]() ,Sn=a1+a2+…+an , 在S1 , S2 , …S100中,正数的个数是( )
,Sn=a1+a2+…+an , 在S1 , S2 , …S100中,正数的个数是( )
A.25
B.50
C.75
D.100
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次模拟考试后,从高三某班随机抽取了20位学生的数学成绩,其分布如下:
分组 | [90,100] | [100,110) | [110,120) | [120,130) | [130,140) | [140,150) |
频数 | 1 | 2 | 6 | 7 | 3 | 1 |
分数在130分(包括130分)以上者为优秀,据此估计该班的优秀率约为( )
A.10%
B.20%
C.30%
D.40%
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 【2017四川宜宾二诊】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,已知点
中,已知点![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为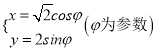 .以原点为极点,
.以原点为极点, ![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为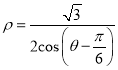 .
.
(Ⅰ)判断点![]() 与直线
与直线![]() 的位置关系并说明理由;
的位置关系并说明理由;
(Ⅱ)设直线![]() 与曲线
与曲线![]() 的两个交点分别为
的两个交点分别为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com