
科目: 来源: 题型:
【题目】电视连续剧《人民的名义》自2017年3月28日在湖南卫视开播以来,引发各方关注,收视率、点击率均占据各大排行榜首位.我们用简单随机抽样的方法对这部电视剧的观看情况进行抽样调查,共调查了600人,得到结果如下:其中图1是非常喜欢《人民的名义》这部电视剧的观众年龄的频率分布直方图;表1是不同年龄段的观众选择不同观看方式的人数.
表1
观看方式 | 电视 | 网络 |
| 150 | 250 |
| 120 | 80 |
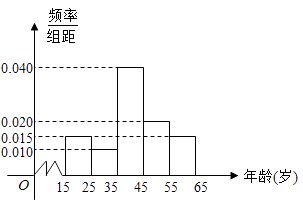
求:(I)假设同一组中的每个数据用该组区间的中点值代替,求非常喜欢《人民的名义》这部电视剧的观众的平均年龄;
(II)根据表1,通过计算说明我们是否有99%的把握认为观看该剧的方式与年龄有关?
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
附: ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知数列 ![]() 的前
的前 ![]() 项和为
项和为 ![]() ,且满足
,且满足 ![]() ,求数列
,求数列 ![]() 的通项公式.勤于思考的小红设计了下面两种解题思路,请你选择其中一种并将其补充完整.
的通项公式.勤于思考的小红设计了下面两种解题思路,请你选择其中一种并将其补充完整.
思路1:先设 ![]() 的值为1,根据已知条件,计算出
的值为1,根据已知条件,计算出 ![]() ,
, ![]() ,
, ![]() .
.
猜想: ![]() .
.
然后用数学归纳法证明.证明过程如下:
①当 ![]() 时, , 猜想成立
时, , 猜想成立
②假设 ![]() (
( ![]() N*)时,猜想成立,即
N*)时,猜想成立,即 ![]() .
.
那么,当 ![]() 时,由已知
时,由已知 ![]() ,得
,得 ![]() .
.
又 ![]() ,两式相减并化简,得
,两式相减并化简,得 ![]() (用含
(用含 ![]() 的代数式表示).
的代数式表示).
所以,当 ![]() 时,猜想也成立.
时,猜想也成立.
根据①和②,可知猜想对任何 ![]() N*都成立.
N*都成立.
思路2:先设 ![]() 的值为1,根据已知条件,计算出
的值为1,根据已知条件,计算出 ![]() .
.
由已知 ![]() ,写出
,写出 ![]() 与
与 ![]() 的关系式:
的关系式: ![]() ,
,
两式相减,得 ![]() 与
与 ![]() 的递推关系式:
的递推关系式: ![]() .
.
整理: ![]() .
.
发现:数列 ![]() 是首项为 , 公比为的等比数列.
是首项为 , 公比为的等比数列.
得出:数列 ![]() 的通项公式
的通项公式 ![]() , 进而得到
, 进而得到 ![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】为建设美丽乡村,政府欲将一块长12百米,宽5百米的矩形空地ABCD建成生态休闲园,园区内有一景观湖EFG(图中阴影部分),以AB所在直线为x轴,AB的垂直平分线为y轴,建立平面直角坐标系xOy(如图所示).景观湖的边界线符合函数y=x+ ![]() (x>0)模型,园区服务中心P在x轴正半轴上,PO=
(x>0)模型,园区服务中心P在x轴正半轴上,PO= ![]() 百米.
百米. 
(1)若在点O和景观湖边界曲线上一点M之间修建一条休闲长廊OM,求OM的最短长度;
(2)若在线段DE上设置一园区出口Q,试确定Q的位置,使通道PQ最短.
查看答案和解析>>
科目: 来源: 题型:
【题目】在四棱锥P﹣ABCD中,底面ABCD为直角梯形,∠BAD=∠ADC=90°,DC=2AB=2AD,BC⊥PD,E,F分别是PB,BC的中点. 
求证:
(1)PC∥平面DEF;
(2)平面PBC⊥平面PBD.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,AB=![]() ,BC=1,P为△ABC内一点,∠BPC=90°.
,BC=1,P为△ABC内一点,∠BPC=90°.
(1)若PB=![]() ,求PA;
,求PA;
(2)若∠APB=150°,求tan∠PBA.

查看答案和解析>>
科目: 来源: 题型:
【题目】设{an}是公比大于1的等比数列,Sn为数列{an}的前n项和,已知S3=7,
且a1+3,3a2,a3+4构成等差数列.
(1)求数列{an}的通项;
(2)令![]() ,n=1,2,…,求数列{bn}的前n项和Tn .
,n=1,2,…,求数列{bn}的前n项和Tn .
查看答案和解析>>
科目: 来源: 题型:
【题目】随着手机的发展,“微信”越来越成为人们交流的一种方式.某机构对“使用微信交流”的态度进行调查,随机抽取了50人,他们年龄的频数分布及对“使用微信交流”赞成人数如下表.
年龄(单位:岁) |
|
|
|
|
|
|
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 5 | 10 | 12 | 7 | 2 | 1 |
(Ⅰ)若以“年龄”45岁为分界点,由以上统计数据完成下面 ![]() 列联表,并判断是否有99%的把握认为“使用微信交流”的态度与人的年龄有关;
列联表,并判断是否有99%的把握认为“使用微信交流”的态度与人的年龄有关;
年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
赞成 | |||
不赞成 | |||
合计 |
(Ⅱ)若从年龄在 ![]() 和
和 ![]() 的被调查人中按照分层抽样的方法选取6人进行追踪调查,并给予其中3人“红包”奖励,求3人中至少有1人年龄在
的被调查人中按照分层抽样的方法选取6人进行追踪调查,并给予其中3人“红包”奖励,求3人中至少有1人年龄在 ![]() 的概率.
的概率.
参考数据如下:
附临界值表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]() 的观测值:
的观测值: ![]() (其中
(其中 ![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】已知向量m ![]() (sin
(sin ![]() ,1),
,1), ![]() =(1,
=(1, ![]() cos
cos ![]() ),函数f(x)=
),函数f(x)= ![]()
(1)求函数f(x)的最小正周期;
(2)若f(α﹣ ![]() )=
)= ![]() ,求f(2α+
,求f(2α+ ![]() )的值.
)的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com