
����Ŀ�������ֻ��ķ�չ�����š�Խ��Խ��Ϊ���ǽ�����һ�ַ�ʽ.ij�����ԡ�ʹ���Ž�������̬�Ƚ��е��飬�����ȡ��50�ˣ����������Ƶ���ֲ����ԡ�ʹ���Ž��������������±�.
���䣨��λ���꣩ |
|
|
|
|
|
|
Ƶ�� | 5 | 10 | 15 | 10 | 5 | 5 |
������ | 5 | 10 | 12 | 7 | 2 | 1 |
�������ԡ����䡱45��Ϊ�ֽ�㣬������ͳ������������� ![]() �����������ж��Ƿ���99%�İ�����Ϊ��ʹ���Ž�������̬�����˵������йأ�
�����������ж��Ƿ���99%�İ�����Ϊ��ʹ���Ž�������̬�����˵������йأ�
���䲻����45������� | �������45������� | �ϼ� | |
�� | |||
���� | |||
�ϼ� |
�������������� ![]() ��
�� ![]() �ı��������а��շֲ�����ķ���ѡȡ6�˽����ٵ��飬����������3�ˡ��������������3����������1��������
�ı��������а��շֲ�����ķ���ѡȡ6�˽����ٵ��飬����������3�ˡ��������������3����������1�������� ![]() �ĸ���.
�ĸ���.
�ο��������£�
���ٽ�ֵ����
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]() �Ĺ۲�ֵ��
�Ĺ۲�ֵ�� ![]() ������
������ ![]() ��
��
���𰸡��⣺������������ ![]() ��������
��������
���䲻����45������� | �������45������� | �ϼ� | |
�� | 10 | 27 | 37 |
���� | 10 | 3 | 13 |
�� �� | 20 | 30 | 50 |
�������������������ݴ��빫ʽ�õ��� ![]()
������99%�İ�����Ϊ��ʹ���Ž�������̬�����˵������йأ�
���⣺���շֲ����������֪�� ![]() ��ȡ��
��ȡ�� ![]() ���ˣ���
���ˣ���
![]() ��ȡ��
��ȡ�� ![]() ���ˣ�
���ˣ�
��������ȡ��6���У������� ![]() ��2�ˣ�����
��2�ˣ����� ![]() ��4�ˣ�
��4�ˣ�
������ ![]() ��Ϊ
��Ϊ ![]() ��������
�������� ![]() ��Ϊ
��Ϊ ![]() �����6������ȡ3�����������Ϊ��
�����6������ȡ3�����������Ϊ�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� 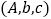 ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��20�������
��20�������
����������һ�������� ![]() ������У�
������� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ����16�������
����16�������
��������һ�������� ![]() ��Ϊ�¼�
��Ϊ�¼� ![]() ����
���� ![]()
��������һ�������� ![]() ��֮��ĸ���Ϊ
��֮��ĸ���Ϊ ![]()
��������(1)��ͼ����֪������������ֵ���жԱȵó����ۡ�(2�����÷ֲ�����ó���ÿ������ε�����Ϊ6�ˣ����������оٳ���6������ȡ���˵������20�֣����ͬ��ɵ�������һ���� [ 55 , 65 )�������16�֣����ø��ʵĶ��������ֵ���ɡ�
�����㾫����������Ĺؼ���������ֲ���������֪ʶ�������Ƚ������е����е�λ����ij���������־���Ա�����ȣ����ֳ��������ͻ��Σ�Ȼ�����ڸ������ͻ����в��ü����������ϵ�ó����İ취��ȡһ���������������Щ���������������������������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=2 ![]() sin��
sin�� ![]() ��x��cos��
��x��cos�� ![]() ��x��+2cos2��
��x��+2cos2�� ![]() ��x�����أ�0�����Һ���f��x������С������Ϊ�У�
��x�����أ�0�����Һ���f��x������С������Ϊ�У�
��1����ص�ֵ��
��2����f��x�������� ![]() �ϵ����ֵ����Сֵ��
�ϵ����ֵ����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������P��ABCD�У�����ABCDΪ���Σ�CD��AB��AB=2CD��AC��BD��O����ǡ�PAD����ƽ��͵���ABCD��PA��BD����Q�ڲ���PC�ϣ���PQ=2QC��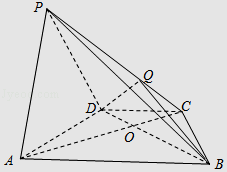
��1����֤��PA��ƽ��QBD��
��2����֤BD��AD��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У���֪��ABC������������ΪA(7��8)��B(10��4)��C(2����4)��
(1)��BC���ϵ���������ֱ�ߵķ��̣�
(2)��BC���ϵĸ�����ֱ�ߵķ��̣�
���𰸡���1��![]() ����2��
����2��![]()
�������������������1�������е����깫ʽ���![]() �е�
�е�![]() �����꣬����б�ʹ�ʽ�����
�����꣬����б�ʹ�ʽ�����![]() ��б�ʣ����õ�бʽ����
��б�ʣ����õ�бʽ����![]() ���ϵ���������ֱ�ߵķ��̣���2���ȸ���б�ʹ�ʽ���
���ϵ���������ֱ�ߵķ��̣���2���ȸ���б�ʹ�ʽ���![]() ��б�ʣ��Ӷ����
��б�ʣ��Ӷ����![]() ���ϵĸ�����ֱ�ߵ�б��Ϊ
���ϵĸ�����ֱ�ߵ�б��Ϊ![]() �����õ�бʽ����
�����õ�бʽ����![]() ���ϵĸ�����ֱ�ߵķ���.
���ϵĸ�����ֱ�ߵķ���.
�����������1����B(10��4)��C(2����4)����BC�е�D������Ϊ��6��0����
����AD��б��Ϊk��![]() ��8��
��8��
����BC���ϵ�����AD����ֱ�ߵķ���Ϊy��0��8(x��6)��
��8x��y��48��0��
��2����B(10��4)��C(2����4)����BC����ֱ�ߵ�б��Ϊk��![]() ��1��
��1��
����BC���ϵĸ�����ֱ�ߵ�б��Ϊ��1��
����BC���ϵĸ�����ֱ�ߵķ���Ϊy��8����(x��7)����x��y��15��0��
�����͡������
��������
17
����Ŀ����ֱ֪��l��x��2y��2m��2��0��
(1)�����(2��3)����ֱ��l��ֱ��ֱ�ߵķ��̣�
(2)��ֱ��l������������Χ�ɵ������ε��������4����ʵ��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У���֪��P��0��1����ԲC��x2+y2+2mx��2y+m2��4m+1=0�ڣ������ڹ���P��ֱ�߽�ԲC��A��B���㣬�ҡ�PBC������ǡ�PAC�������2������ʵ��m��ȡֵ��ΧΪ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���� ![]() ��ǰ
��ǰ ![]() ���Ϊ
���Ϊ ![]() ��������
�������� ![]() ��������
�������� ![]() ��ͨ�ʽ������˼����С��������������ֽ���˼·������ѡ������һ�ֲ����䲹��������
��ͨ�ʽ������˼����С��������������ֽ���˼·������ѡ������һ�ֲ����䲹��������
˼·1������ ![]() ��ֵΪ1��������֪�����������
��ֵΪ1��������֪����������� ![]() ��
�� ![]() ��
�� ![]() ��
��
���룺 ![]() .
.
Ȼ������ѧ���ɷ�֤����֤���������£�
�ٵ� ![]() ʱ�� �� �������
ʱ�� �� �������
�ڼ��� ![]() ��
�� ![]() N*��ʱ�������������
N*��ʱ������������� ![]() ��
��
��ô���� ![]() ʱ������֪
ʱ������֪ ![]() ����
���� ![]() ��
��
�� ![]() ����ʽ���������
����ʽ��������� ![]() ���ú�
���ú� ![]() �Ĵ���ʽ��ʾ����
�Ĵ���ʽ��ʾ����
���ԣ��� ![]() ʱ������Ҳ������
ʱ������Ҳ������
���ݢٺ͢ڣ���֪������κ� ![]() N*��������
N*��������
˼·2������ ![]() ��ֵΪ1��������֪�����������
��ֵΪ1��������֪����������� ![]() ��
��
����֪ ![]() ��д��
��� ![]() ��
�� ![]() �Ĺ�ϵʽ��
�Ĺ�ϵʽ�� ![]() ��
��
��ʽ������� ![]() ��
�� ![]() �ĵ��ƹ�ϵʽ��
�ĵ��ƹ�ϵʽ�� ![]() ��
��
������ ![]() ��
��
���֣����� ![]() ������Ϊ �� ����Ϊ�ĵȱ����У�
������Ϊ �� ����Ϊ�ĵȱ����У�
�ó������� ![]() ��ͨ�ʽ
��ͨ�ʽ ![]() �� �����õ�
�� �����õ� ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��һϵ�ж�Ӧֵ���±���
��һϵ�ж�Ӧֵ���±���

��1�����ݱ����ṩ�������������![]() ��һ������ʽ��
��һ������ʽ��
��2�����ݣ�1���Ľ����������![]() ������Ϊ
������Ϊ![]() ����
����![]() ʱ������
ʱ������![]() ǡ��������ͬ�Ľ⣬��ʵ��
ǡ��������ͬ�Ľ⣬��ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2017��1��18�տ�ʼ��֧�����û�����ͨ����![]() ɨ�������֡��͡���������ɭ�֡����ַ�ʽ��ø���(����������ǿ������г�������Ƹ�����ҵ��������Ϧҹ
ɨ�������֡��͡���������ɭ�֡����ַ�ʽ��ø���(����������ǿ������г�������Ƹ�����ҵ��������Ϧҹ![]() ��ÿһλ��ǰ�����帣���û��������һ���ֽ���.ij�{Уһ�����������ѧ�����������80λ��У�ڶ���ѧ�����ͳ�Ϧҹ
��ÿһλ��ǰ�����帣���û��������һ���ֽ���.ij�{Уһ�����������ѧ�����������80λ��У�ڶ���ѧ�����ͳ�Ϧҹ![]() ֮ǰ�Ƿ����帣������һ�ε���(��δ���뼯�帣�Ļ����Ҳ��ͬ��δ�����帣�����õ������������±�:
֮ǰ�Ƿ����帣������һ�ε���(��δ���뼯�帣�Ļ����Ҳ��ͬ��δ�����帣�����õ������������±�:
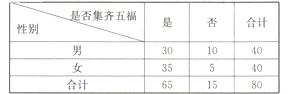
��1��������80λ��ѧ�������帣��Ƶ�ʣ����ݴ˹����У10000���ڶ���ѧ���м����帣��������
��2��Ϊ�˽⼯���帣�Ĵ�ѧ�������Ƿ�Ը������μӼ��帣����ô�ѧ��ѧ����Ӽ����帣��ѧ���У�ѡȡ2λ������3λŮ��������вɷã���������ѡȡ3�βɷü�¼�ŵ��ô�ѧ�Ĺٷ���վ�ϣ������ѡȡ��3�βɷö�����������һλ�����ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������f��x��=Asin��x+�գ���A��0��0����4��|��|�� ![]() �����㣨0��
�����㣨0�� ![]() �����ҵ�x=
�����ҵ�x= ![]() ʱ������f��x��ȡ�����ֵ1��
ʱ������f��x��ȡ�����ֵ1��
��1��������f��x����ͼ������ƽ�� ![]() ����λ�õ�����g��x��������g��x���ı���ʽ��
����λ�õ�����g��x��������g��x���ı���ʽ��
��2���ڣ�1���������£�����h��x��=f��x��+g��x��+2cos2x��1���������x1 �� x2��R������h��x1����h��x����h��x2������|x1��x2|����Сֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com