
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD为梯形,CD∥AB,AB=2CD,AC交BD于O,锐角△PAD所在平面⊥底面ABCD,PA⊥BD,点Q在侧棱PC上,且PQ=2QC.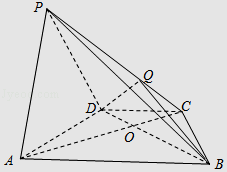
(1)求证:PA∥平面QBD;
(2)求证BD⊥AD.
【答案】
(1)证明:如图,连接OQ,因为AB∥CD,AB=2 CD,
所以AO=2OC,又PQ=2QC,
所以PA∥OQ,
又OQ平面QBD,PA平面QBD,
所以PA∥平面QBD
(2)
证明:在平面PAD内过P作PH⊥AD于H,因为侧面PAD⊥底面ABCD,平面PAD∩平面ABCD=AD, PH平面PAD,所以PH⊥平面ABCD
又BD平面ABCD,所以PH⊥BD,又PA⊥BD,
且PA和PH是平面PAD内的两条相交直线,所以BD⊥平面PAD,
又AD平面PAD,所以BD⊥AD.
【解析】(1)连接OQ,可得PA∥OQ,即可证得PA∥平面QBD.
(2)在平面PAD内过P作PH⊥AD于H,可得PH⊥平面ABCD,即可得PH⊥BD,可得到以BD⊥平面PAD,即BD⊥AD.
【考点精析】本题主要考查了直线与平面平行的判定和直线与平面垂直的性质的相关知识点,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;垂直于同一个平面的两条直线平行才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】如图,在△ABC中,已知A(5,-2),B(7,3),且AC边的中点M在y轴上,BC的中点N在x轴上.

(1)求点C的坐标;
(2)求![]() 边上的中线所在直线方程.
边上的中线所在直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是异面直线,则以下四个命题:①存在分别经过直线
是异面直线,则以下四个命题:①存在分别经过直线![]() 和
和![]() 的两个互相垂直的平面;②存在分别经过直线
的两个互相垂直的平面;②存在分别经过直线![]() 和
和![]() 的两个平行平面;③经过直线
的两个平行平面;③经过直线![]() 有且只有一个平面垂直于直线
有且只有一个平面垂直于直线![]() ;④经过直线
;④经过直线![]() 有且只有一个平面平行于直线
有且只有一个平面平行于直线![]() ,其中正确的个数有( )
,其中正确的个数有( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查喜欢旅游是否与性别有关,调查人员就“是否喜欢旅游”这个问题,在火车站分别随机调研了 ![]() 名女性或
名女性或 ![]() 名男性,根据调研结果得到如图所示的等高条形图.
名男性,根据调研结果得到如图所示的等高条形图.
(1)完成下列 ![]() 列联表:
列联表:
喜欢旅游 | 不喜欢旅游 | 估计 | |
女性 | |||
男性 | |||
合计 |
(2)能否在犯错误概率不超过 ![]() 的前提下认为“喜欢旅游与性别有关”.
的前提下认为“喜欢旅游与性别有关”.
附:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考公式:![]() ,其中
,其中 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,
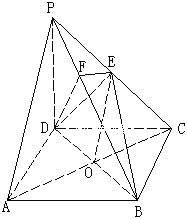
(1)证明:PA∥平面EDB
(2)证明:平面BDE![]() 平面PCB
平面PCB
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系 ![]() 中,以
中,以 ![]() 为极点,
为极点, ![]() 轴的正半轴为极轴,建立极坐标系.曲线
轴的正半轴为极轴,建立极坐标系.曲线 ![]() 的极坐标方程为
的极坐标方程为 ![]() ,曲线
,曲线 ![]() 的参数方程为
的参数方程为 ![]() (
( ![]() 为参数),
为参数), ![]() .
.
(Ⅰ)求曲线 ![]() 的直角坐标方程,并判断该曲线是什么曲线?
的直角坐标方程,并判断该曲线是什么曲线?
(Ⅱ)设曲线 ![]() 与曲线
与曲线 ![]() 的交点为
的交点为 ![]() ,
, ![]() ,
, ![]() ,当
,当 ![]() 时,求
时,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着手机的发展,“微信”越来越成为人们交流的一种方式.某机构对“使用微信交流”的态度进行调查,随机抽取了50人,他们年龄的频数分布及对“使用微信交流”赞成人数如下表.
年龄(单位:岁) |
|
|
|
|
|
|
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 5 | 10 | 12 | 7 | 2 | 1 |
(Ⅰ)若以“年龄”45岁为分界点,由以上统计数据完成下面 ![]() 列联表,并判断是否有99%的把握认为“使用微信交流”的态度与人的年龄有关;
列联表,并判断是否有99%的把握认为“使用微信交流”的态度与人的年龄有关;
年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
赞成 | |||
不赞成 | |||
合计 |
(Ⅱ)若从年龄在 ![]() 和
和 ![]() 的被调查人中按照分层抽样的方法选取6人进行追踪调查,并给予其中3人“红包”奖励,求3人中至少有1人年龄在
的被调查人中按照分层抽样的方法选取6人进行追踪调查,并给予其中3人“红包”奖励,求3人中至少有1人年龄在 ![]() 的概率.
的概率.
参考数据如下:
附临界值表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]() 的观测值:
的观测值: ![]() (其中
(其中 ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的半焦距为
的半焦距为 ![]() ,原点
,原点 ![]() 到经过两点
到经过两点 ![]() 的直线的距离为
的直线的距离为 ![]() .
.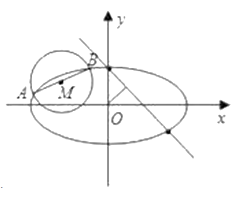
(Ⅰ)求椭圆 ![]() 的离心率;
的离心率;
(Ⅱ)如图, ![]() 是圆
是圆 ![]() 的一条直径,若椭圆
的一条直径,若椭圆 ![]() 经过
经过 ![]() 两点,求椭圆
两点,求椭圆 ![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com