
【题目】如图,在△ABC中,已知A(5,-2),B(7,3),且AC边的中点M在y轴上,BC的中点N在x轴上.

(1)求点C的坐标;
(2)求![]() 边上的中线所在直线方程.
边上的中线所在直线方程.
【答案】(1)(-5,-3);(2)7x-22y-31=0.
【解析】试题分析:(1)根据题意得到可设设M(0,a),N(b,0),C(m,n), ∵A(5,-2),B(7,3),
根据中点坐标公式得到点C的坐标;(2)根据中点坐标公式得到点![]() 的坐标为
的坐标为![]() ,由两点式得到AB中线所在直线的方程.
,由两点式得到AB中线所在直线的方程.
解析:
(1)设M(0,a),N(b,0),C(m,n), ∵A(5,-2),B(7,3),
又M是AC的中点,∴5+m=0,m=-5,
N是BC的中点,∴3+n=0,n=-3,
∴C点坐标为(-5,-3),
(2)设AB的中点为![]() ,则点
,则点![]() 的坐标为
的坐标为![]()
由两点式得AB边中线所在直线方程为
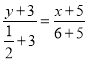
整理得:7x-22y-31=0.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知 ![]() ,B(0,2),C(1,0),斜率为
,B(0,2),C(1,0),斜率为 ![]() 的直线l过点A,且l和以C为圆心的圆相切.
的直线l过点A,且l和以C为圆心的圆相切.
(1)求圆C的方程;
(2)在圆C上是否存在点P,使得 ![]() ,若存在,求出所有的点P的坐标;若不存在说明理由;
,若存在,求出所有的点P的坐标;若不存在说明理由;
(3)若不过C的直线m与圆C交于M,N两点,且满足CM,MN,CN的斜率依次为等比数列,求直线m的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,△ABC是圆的内接三角形,∠BAC的平分线交圆于点D,交BC于E,过点B的圆的切线与AD的延长线交于点F,在上述条件下,给出下列四个结论:
①BD平分∠CBF;
②FB2=FDFA;
③AECE=BEDE;
④AFBD=ABBF.
所有正确结论的序号是( )
A.①②
B.③④
C.①②③
D.①②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场举行有奖促销活动,顾客购买一定金额商品后即可抽奖,每次抽奖都从装有4个红球、6个白球的甲箱和装有5个红球、5个白球的乙箱中,各随机摸出1个球,在摸出的2个球中,若都是红球,则获一等奖;若只有1个红球,则获二等奖;若没有红球,则不获奖.
(1)求顾客抽奖1次能获奖的概率;
(2)若某顾客有3次抽奖机会,记该顾客在3次抽奖中获一等奖的次数为x,求x的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数集![]() 具有性质
具有性质![]() :对任意的
:对任意的![]()
![]() ,
,![]() ,使得
,使得![]() 成立.
成立.
(Ⅰ)分别判断数集![]() 与
与![]() 是否具有性质
是否具有性质![]() ,并说明理由;
,并说明理由;
(Ⅱ)求证![]() ;
;
(Ⅲ)若![]() ,求数集
,求数集![]() 中所有元素的和的最小值.
中所有元素的和的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,△ABC是等腰直角三角形∠CAB=90°,AC=2a,E,F分别为AC,BC的中点,沿EF将△CEF折起,得到如图2所示的四棱锥C′﹣ABFE
(1)求证:AB⊥平面AEC′;
(2)当四棱锥C′﹣ABFE体积取最大值时,
①若G为BC′中点,求异面直线GF与AC′所成角;
②在C′﹣ABFE中AE交BF于C,求二面角A﹣CC′﹣B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2 ![]() sin(
sin( ![]() ωx)cos(
ωx)cos( ![]() ωx)+2cos2(
ωx)+2cos2( ![]() ωx)(ω>0),且函数f(x)的最小正周期为π.
ωx)(ω>0),且函数f(x)的最小正周期为π.
(1)求ω的值;
(2)求f(x)在区间 ![]() 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD为梯形,CD∥AB,AB=2CD,AC交BD于O,锐角△PAD所在平面⊥底面ABCD,PA⊥BD,点Q在侧棱PC上,且PQ=2QC.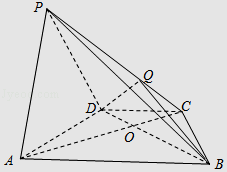
(1)求证:PA∥平面QBD;
(2)求证BD⊥AD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com