【题目】某地要建造一个边长为2（单位：km）的正方形市民休闲公园OABC，将其中的区域ODC开挖成一个池塘，如图建立平面直角坐标系后，点D的坐标为（1，2），曲线OD是函数y=ax2图象的一部分，对边OA上一点M在区域OABD内作一次函数y=kx+b（k＞0）的图象，与线段DB交于点N（点N不与点D重合），且线段MN与曲线OD有且只有一个公共点P，四边形MABN为绿化风景区：
（1）求证：b=﹣ ；
（2）设点P的横坐标为t，①用t表示M、N两点坐标；②将四边形MABN的面积S表示成关于t的函数S=S（t），并求S的最大值．

【题目】在△ABC中，a，b，c分别是角A，B，C的对边，且8sin2 ．
（1）求角A的大小；
（2）若a= ，b+c=3，求b和c的值．

【题目】如图，已知AB⊥平面BCD，BC⊥CD，AD与平面BCD所成的角为30°，且AB=BC=2；
（1）求三棱锥A﹣BCD的体积；
（2）设M为BD的中点，求异面直线AD与CM所成角的大小（结果用反三角函数值表示）．

【题目】已知无穷数列{an}的各项都是正数，其前n项和为Sn ， 且满足：a1=a，rSn=anan+1﹣1，其中a≠1，常数r∈N；
（1）求证：an+2﹣an是一个定值；
（2）若数列{an}是一个周期数列（存在正整数T，使得对任意n∈N* ， 都有an+T=an成立，则称{an}为周期数列，T为它的一个周期，求该数列的最小周期；
（3）若数列{an}是各项均为有理数的等差数列，cn=23n﹣1（n∈N*），问：数列{cn}中的所有项是否都是数列{an}中的项？若是，请说明理由，若不是，请举出反例．

某单位建造一间地面面积为12m2的背面靠墙的矩形小房，由于地理位置的限制，房子侧面的长度x不得超过米，房屋正面的造价为400元/m2,房屋侧面的造价为150元/m2，屋顶和地面的造价费用合计为5800元，如果墙高为3m，且不计房屋背面的费用．

（1）把房屋总造价表示成的函数，并写出该函数的定义域.

（2）当侧面的长度为多少时，总造价最底？最低总造价是多少？

【题目】已知函数f（x）=9x﹣2a3x+3：
（1）若a=1，x∈[0，1]时，求f（x）的值域；
（2）当x∈[﹣1，1]时，求f（x）的最小值h（a）；
（3）是否存在实数m、n，同时满足下列条件：①n＞m＞3；②当h（a）的定义域为[m，n]时，其值域为[m2 ， n2]，若存在，求出m、n的值，若不存在，请说明理由．

【题目】某地要建造一个边长为2（单位：km）的正方形市民休闲公园OABC，将其中的区域ODC开挖成一个池塘，如图建立平面直角坐标系后，点D的坐标为（1，2），曲线OD是函数y=ax2图象的一部分，对边OA上一点M在区域OABD内作一次函数y=kx+b（k＞0）的图象，与线段DB交于点N（点N不与点D重合），且线段MN与曲线OD有且只有一个公共点P，四边形MABN为绿化风景区：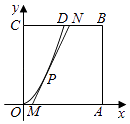
（1）求证：b=﹣ ；
（2）设点P的横坐标为t，①用t表示M、N两点坐标；②将四边形MABN的面积S表示成关于t的函数S=S（t），并求S的最大值．

【题目】在△ABC中，a，b，c分别是角A，B，C的对边，且8sin2 ．
（1）求角A的大小；
（2）若a= ，b+c=3，求b和c的值．

【题目】如图，已知AB⊥平面BCD，BC⊥CD，AD与平面BCD所成的角为30°，且AB=BC=2；
（1）求三棱锥A﹣BCD的体积；
（2）设M为BD的中点，求异面直线AD与CM所成角的大小（结果用反三角函数值表示）．

【题目】设向量 =（1，﹣2）， =（a，﹣1）， =（﹣b，0），其中O为坐标原点，a＞0，b＞0，若A、B、C三点共线，则 的最小值为 ．