【题目】设函数．

（）若，求函数的单调区间．

（）若函数在区间上是减函数，求实数的取值范围．

（）过坐标原点作曲线的切线，证明：切点的横坐标为．

【题目】在平面角坐标系中，以坐标原点为极点， 轴的正半轴为极轴建立极坐标系，已知曲线的极坐标方程为，将曲线向左平移个单位长度得到曲线.

（1）求曲线的参数方程；

（2）已知为曲线上的动点， 两点的极坐标分别为，求的最大值.

【题目】如图，在四棱锥中，底面为梯形，平面平面

为侧棱的中点，且.

（1）证明： 平面；

（2）若点到平面的距离为，且，求点到平面的距离.

【题目】【2018届山西省太原十二中高三上学期1月月考】运动员甲在最近场比赛中所得分数的茎叶图如图所示，由于疏忽，茎叶图中的两个数据上出行了污渍，导致这两个数字无法辨认，但统计员记得除掉污渍处的数字不影响整体中位数，且这六个数据的平均值为.

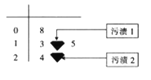
（1）求污渍处的数字；

（2）篮球运动员乙在最近场的比赛中所得分数为.试分别以各自场比赛得分的平均数与方差来分析这两名篮球运动员的发挥水平.

【题目】设S是实数集R的非空子集，若对任意x，y∈S，都有x＋y，x－y，xy∈S，则称S为封闭集．下列命题：①集合S＝{a＋b|a，b为整数}为封闭集；②若S为封闭集，则一定有0∈S；③封闭集一定是无限集；④若S为封闭集，则满足STR的任意集合T也是封闭集．其中真命题是________．(写出所有真命题的序号)

【题目】用C(A)表示非空集合A中的元素个数，定义A*B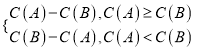＝若A＝{1,2}，B＝{x|(x2＋ax)·(x2＋ax＋2)＝0}，且A*B＝1，设实数a的所有可能取值组成的集合是S，则C(S)等于(　　)

A. 1 B. 3

C. 5 D. 7

【题目】已知函数， ．

（Ⅰ）求曲线在点处的切线的斜率；

（Ⅱ）判断方程（为的导数）在区间内的根的个数，说明理由；

（Ⅲ）若函数在区间内有且只有一个极值点，求的取值范围．

【题目】已知椭圆的一个焦点坐标为．

（Ⅰ）求椭圆的方程；

（Ⅱ）已知点，过点的直线（与轴不重合）与椭圆交于两点，直线与直线相交于点，试证明：直线与轴平行．

【题目】如图，在三棱柱中，底面为正三角形，侧棱底面．已知是的中点， ．

（Ⅰ）求证：平面平面；

（Ⅱ）求证：∥平面；

（Ⅲ）求三棱锥的体积．

图1

选手乙的接发球技术统计表

表1

（Ⅰ）观察图1，在两位选手共同使用的8项技术中，差异最为显著的是哪两项技术？

（Ⅱ）乒乓球接发球技术中的拉球技术包括正手拉球和反手拉球．从表1统计的选手乙的所有拉球中任取两次，至少抽出一次反手拉球的概率是多少？

（Ⅲ）如果仅从表1中选手乙接发球得分率的稳定性来看（不考虑使用次数），你认为选手乙的反手技术更稳定还是正手技术更稳定？（结论不要求证明）