
科目: 来源: 题型:
【题目】某公司为了激励业务员的积极性,对业绩在60万到200万的业务员进行奖励奖励方案遵循以下原则:奖金y(单位:万元)随着业绩值x(单位:万元)的增加而增加,且奖金不低于1.5万元同时奖金不超过业绩值的5%.
(1)若某业务员的业绩为100万核定可得4万元奖金,若该公司用函数![]() (k为常数)作为奖励函数模型,则业绩200万元的业务员可以得到多少奖励?(已知
(k为常数)作为奖励函数模型,则业绩200万元的业务员可以得到多少奖励?(已知![]() ,
,![]() )
)
(2)若采用函数![]() 作为奖励函数模型试确定最小的正整数a的值.
作为奖励函数模型试确定最小的正整数a的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】孝感市旅游局为了了解双峰山景点在大众中的熟知度,从年龄在15~65岁的人群中随机抽取![]() 人进行问卷调查,把这
人进行问卷调查,把这![]() 人按年龄分成5组:第一组
人按年龄分成5组:第一组![]() ,第二组
,第二组![]() ,第三组
,第三组![]() ,第四组
,第四组![]() ,第五组
,第五组![]() ,得到的样本的频率分布直方图如图:
,得到的样本的频率分布直方图如图:
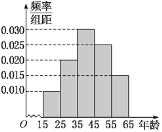
调查问题是“双峰山国家森林公园是几![]() 级旅游景点?”每组中回答正确的人数及回答正确的人数占本组的频率的统计结果如下表.
级旅游景点?”每组中回答正确的人数及回答正确的人数占本组的频率的统计结果如下表.
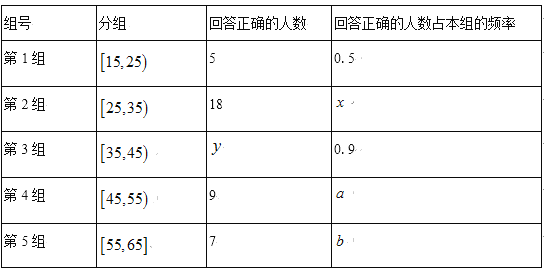
(1)分别求出![]() 的值;
的值;
(2)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,求第2,3,4组每组各抽取多少人;
(3)在(2)抽取的6人中随机抽取2人,求所抽取的两人来自不同年龄组的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系中,直线l的参数方程为![]() (t为参数,
(t为参数,![]() ),以坐标原点为极点,
),以坐标原点为极点,![]() 轴正半轴为极轴,取相同的长度单位建立极坐标系,曲线C的极坐标方程为
轴正半轴为极轴,取相同的长度单位建立极坐标系,曲线C的极坐标方程为![]() .
.
(1)当![]() 时,写出直线l的普通方程及曲线C的直角坐标方程;
时,写出直线l的普通方程及曲线C的直角坐标方程;
(2)已知点![]() ,设直线l与曲线C交于A,B两点,试确定
,设直线l与曲线C交于A,B两点,试确定![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了解本市的交通状况,某校高一年级的同学分成了甲、乙、丙三个组,从下午13点到18点,分别对三个路口的机动车通行情况进行了实际调查,并绘制了频率分布直方图(如图),记甲、乙、丙三个组所调查数据的标准差分别为![]() ,则它们的大小关系为( )
,则它们的大小关系为( )



A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】设抛物线![]() 的焦点为F,已知直线
的焦点为F,已知直线![]() 与抛物线C交于A,B两点(A,B两点分别在
与抛物线C交于A,B两点(A,B两点分别在![]() 轴的上、下方).
轴的上、下方).
(1)求证:![]() ;
;
(2)已知弦长![]() ,试求:过A,B两点,且与直线
,试求:过A,B两点,且与直线![]() 相切的圆D的方程.
相切的圆D的方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知定义在R上的偶函数f(x)和奇函数g(x)满足![]() .
.
(1)求函数f(x)和g(x)的表达式;
(2)当![]() 时,不等式
时,不等式![]() 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;
(3)若方程![]() 在
在![]() 上恰有一个实根,求实数m的取值范围.
上恰有一个实根,求实数m的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,底面为菱形的直四棱柱![]() 被过三点
被过三点![]() 的平面截去一个三棱锥
的平面截去一个三棱锥![]() (图一)得几何体
(图一)得几何体![]() (图二),E为
(图二),E为![]() 的中点.
的中点.
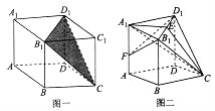
(1)点F为棱![]() 上的动点,试问平面
上的动点,试问平面![]() 与平面
与平面![]() 是否垂直?请说明理由;
是否垂直?请说明理由;
(2)设![]() ,当点F为
,当点F为![]() 中点时,求锐二面角
中点时,求锐二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】若函数![]() 对定义域内的每一个值
对定义域内的每一个值![]() ,在其定义域内都存在唯一的
,在其定义域内都存在唯一的![]() ,使
,使![]() 成立,则该函数为“依附函数”.
成立,则该函数为“依附函数”.
(1)判断函数![]() 是否为“依附函数”,并说明理由;
是否为“依附函数”,并说明理由;
(2)若函数![]() 在定义域
在定义域![]() 上“依附函数”,求
上“依附函数”,求![]() 的取值范围;
的取值范围;
(3)已知函数![]() 在定义域
在定义域![]() 上为“依附函数”.若存在实数
上为“依附函数”.若存在实数![]() ,使得对任意的
,使得对任意的![]() ,不等式
,不等式![]() 都成立,求实数
都成立,求实数![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com