
【题目】已知函数![]() .
.
(1)若![]() ,证明:当
,证明:当![]() ;
;
(2)设![]() ,若函数
,若函数![]() 上有2个不同的零点,求实数
上有2个不同的零点,求实数![]() 的取值范围.
的取值范围.
【答案】(1)见解析;(2)![]()
【解析】
(1) 当a=1时.![]() .
. ![]() 明确单调性求出最大值即可;(2)
明确单调性求出最大值即可;(2)![]() ,讨论a的范围,易知当
,讨论a的范围,易知当![]() 时,
时,![]() 没有零;当
没有零;当![]() 时,研究函数
时,研究函数![]() 的单调性,明确图象与x轴的交点情况即可.
的单调性,明确图象与x轴的交点情况即可.
(1)当a=1时.![]() .
.
![]() .
.
因为![]() ,所以
,所以![]() ,
,
所以![]() 在
在![]() 时单调递减,
时单调递减,
所以![]() ,即
,即![]() .
.
(2)法一:![]()
(i)当![]() 时,
时,![]() 没有零;
没有零;
(ii)当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
故![]() 是
是![]() 在
在![]() 上的最小值
上的最小值
①若![]() ,即
,即![]() 时,
时,![]() 在
在![]() 上没有零点;
上没有零点;
②若![]() ,即
,即![]() 时,
时,![]() 在
在![]() 上只有1个零点;
上只有1个零点;
③若![]() ,即
,即![]() 时,由于
时,由于![]() ,所以
,所以![]() 在(0,2)上有1个零点,
在(0,2)上有1个零点,
由(1)知,当![]() 时,
时,![]() ,
,
因为![]() ,
,
所以![]() .
.
故![]() 在(2,4a)上有1个零点,因此
在(2,4a)上有1个零点,因此![]() 在
在![]() 上有2个不同的零点。
上有2个不同的零点。
综上,![]() 在
在![]() 上有2个不同的零点时,a的取值范围是
上有2个不同的零点时,a的取值范围是![]() .
.
法二:因为![]() ,
,
所以![]() 在
在![]() 上零点的个数即为方程
上零点的个数即为方程![]() 在
在![]() 上根的个数。
上根的个数。
令![]() .
.
则![]() ,
,
令![]() 得x=2.
得x=2.
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
所以当![]() 时,
时,![]() 单调递增,
单调递增,
当![]() 时,
时,![]() 单调递减,
单调递减,
所以![]() 在
在![]() 上的最大值为
上的最大值为![]() ,
,
由(1)知,当![]() 时,
时,![]() ,
,
即当![]() 时,
时,![]()
因为当x无限增大时,![]() →0,所以当x无限增大时,
→0,所以当x无限增大时,![]() →0,
→0,
又因为![]() ,所以当且仅当
,所以当且仅当![]() 时,
时,
函数![]() 在
在![]() 上的图象与直线
上的图象与直线![]() 恰好有2个不同的交点,
恰好有2个不同的交点,
即当且仅当a>一时,函数h(x)在(0,+oo)上有2个不同的零点,
故![]() 在
在![]() 上有2个不同的零点时,a的取值范围是
上有2个不同的零点时,a的取值范围是![]()


科目:高中数学 来源: 题型:
【题目】某高校在2012年的自主招生考试成绩中随机抽取![]() 名中学生的笔试成绩,按成绩分组,得到的频率分布表如表所示.
名中学生的笔试成绩,按成绩分组,得到的频率分布表如表所示.
组号 | 分组 | 频数 | 频率 |
第1组 |
| 5 |
|
第2组 |
| ① |
|
第3组 |
| 30 | ② |
第4组 |
| 20 |
|
第5组 |
| 10 |
|

(1)请先求出频率分布表中![]() 位置的相应数据,再完成频率分布直方图;
位置的相应数据,再完成频率分布直方图;
(2)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第![]() 组中用分层抽样抽取名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试;
组中用分层抽样抽取名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试;
(3)在(2)的前提下,学校决定在![]() 名学生中随机抽取
名学生中随机抽取![]() 名学生接受
名学生接受![]() 考官进行面试,求:第
考官进行面试,求:第![]() 组至少有一名学生被考官
组至少有一名学生被考官![]() 面试的概率.
面试的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种产品的广告费支出x(单位:百万元)与销售额y(单位:百万元)之间有如下的对应数据:
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | 50 | 70 |
(1)画出散点图;
(2)求y关于x的线性回归方程.
(3)如果广告费支出为一千万元,预测销售额大约为多少百万元?
参考公式用最小二乘法求线性回归方程系数公式: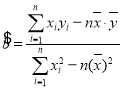 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对下列命题:
①直线![]() 与函数
与函数![]() 的图象相交,则相邻两交点的距离为
的图象相交,则相邻两交点的距离为![]() ;
;
②点![]() 是函数
是函数![]() 的图象的一个对称中心;
的图象的一个对称中心;
③函数![]() 在
在![]() 上单调递减,则
上单调递减,则![]() 的取值范围为
的取值范围为![]() ;
;
④函数![]() 若
若![]() 对
对![]() R恒成立,则
R恒成立,则![]() .
.
其中所有正确命题的序号为____
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 对定义域内的每一个值
对定义域内的每一个值![]() ,在其定义域内都存在唯一的
,在其定义域内都存在唯一的![]() ,使
,使![]() 成立,则该函数为“依附函数”.
成立,则该函数为“依附函数”.
(1)判断函数![]() 是否为“依附函数”,并说明理由;
是否为“依附函数”,并说明理由;
(2)若函数![]() 在定义域
在定义域![]() 上“依附函数”,求
上“依附函数”,求![]() 的取值范围;
的取值范围;
(3)已知函数![]() 在定义域
在定义域![]() 上为“依附函数”.若存在实数
上为“依附函数”.若存在实数![]() ,使得对任意的
,使得对任意的![]() ,不等式
,不等式![]() 都成立,求实数
都成立,求实数![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 的焦点是椭圆
的焦点是椭圆![]() :
: ![]() (
(![]() )的顶点,且椭圆与双曲线的离心率互为倒数.
)的顶点,且椭圆与双曲线的离心率互为倒数.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设动点![]() ,
, ![]() 在椭圆
在椭圆![]() 上,且
上,且![]() ,记直线
,记直线![]() 在
在![]() 轴上的截距为
轴上的截距为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)![]() (k>0)
(k>0)
(1)若f(x)>m的解集为{x|x<-3,或x>-2},求不等式5mx2+kx+3>0的解集;
(2)若存在x>3,使得f(x)>1成立,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】推进垃圾分类处理,是落实绿色发展理念的必然选择,也是打赢污染防治攻坚战的重要环节.为了解居民对垃圾分类的了解程度某社区居委会随机抽取1000名社区居民参与问卷测试,并将问卷得分绘制频率分布表如表:
得分 | [30,40) | [40,50) | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
男性人数 | 40 | 90 | 120 | 130 | 110 | 60 | 30 |
女性人数 | 20 | 50 | 80 | 110 | 100 | 40 | 20 |
(1)从该社区随机抽取一名居民参与问卷测试试估计其得分不低于60分的概率:
(2)将居民对垃圾分类的了解程度分为“比较了解”(得分不低于60分)和“不太了解”(得分低于60)两类,完成2×2列联表,并判断是否有95%的把握认为“居民对垃圾分类的了解程度”与“性别”有关?
不太了解 | 比较了解 | 合计 | |
男性 | |||
女性 | |||
合计 |
(3)从参与问卷测试且得分不低于80分的居民中,按照性别进行分层抽样,共抽取10人,现从这10人中随机抽取3人作为环保宣传队长,设3人中男性队长的人数为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
附:![]() .
.
临界值表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com