
科目: 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).M是曲线
为参数).M是曲线![]() 上的动点,将线段OM绕O点顺时针旋转
上的动点,将线段OM绕O点顺时针旋转![]() 得到线段ON,设点N的轨迹为曲线
得到线段ON,设点N的轨迹为曲线![]() .以坐标原点O为极点,
.以坐标原点O为极点,![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)在(1)的条件下,若射线![]() 与曲线
与曲线![]() 分别交于A, B两点(除极点外),且有定点
分别交于A, B两点(除极点外),且有定点![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=ex+e-x,g(x)=2x+ax3,a为实常数.
(1)求g(x)的单调区间;
(2)当a=-1时,证明:存在x0∈(0,1),使得y=f(x)和y=g(x)的图象在x=x0处的切线互相平行.
查看答案和解析>>
科目: 来源: 题型:
【题目】近期,某超市针对一款饮料推出刷脸支付活动,活动设置了一段时间的推广期,由于推广期内优惠力度较大,吸引越来越多的人开始使用刷脸支付.该超市统计了活动刚推出一周内每一天使用刷脸支付的人次,用![]() 表示活动推出的天数,
表示活动推出的天数,![]() 表示每天使用刷脸支付的人次,统计数据如下表所示:
表示每天使用刷脸支付的人次,统计数据如下表所示:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)在推广期内,![]() 与
与![]() (
(![]() 均为大于零的常数)哪一个适宜作为刷脸支付的人次
均为大于零的常数)哪一个适宜作为刷脸支付的人次![]() 关于活动推出天数
关于活动推出天数![]() 的回归方程类型?(给出判断即可,不必说明理由);
的回归方程类型?(给出判断即可,不必说明理由);
(2)根据(1)的判断结果及表![]() 中的数据,求
中的数据,求![]() 关于
关于![]() 的回归方程,并预测活动推出第
的回归方程,并预测活动推出第![]() 天使用刷脸支付的人次;
天使用刷脸支付的人次;
(3)已知一瓶该饮料的售价为![]() 元,顾客的支付方式有三种:现金支付、扫码支付和刷脸支付,其中有
元,顾客的支付方式有三种:现金支付、扫码支付和刷脸支付,其中有![]() 使用现金支付,使用现金支付的顾客无优惠;有
使用现金支付,使用现金支付的顾客无优惠;有![]() 使用扫码支付,使用扫码支付享受
使用扫码支付,使用扫码支付享受![]() 折优惠;有
折优惠;有![]() 使用刷脸支付,根据统计结果得知,使用刷脸支付的顾客,享受
使用刷脸支付,根据统计结果得知,使用刷脸支付的顾客,享受![]() 折优惠的概率为
折优惠的概率为![]() ,享受
,享受![]() 折优惠的概率为
折优惠的概率为![]() ,享受
,享受![]() 折优惠的概率为
折优惠的概率为![]() .根据所给数据估计购买一瓶该饮料的平均花费.
.根据所给数据估计购买一瓶该饮料的平均花费.
参考数据:其中![]() ,
,![]()
|
|
|
|
|
|
参考公式:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为:
![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】数学是研究数量、结构、变化、空间以及信息等概念的一门科学.在人类历史发展和社会生活中,数学发挥着不可替代的作用,也是学习和研究现代科学技术必不可少的基本工具.
(1)为调查大学生喜欢数学命题是否与性别有关,随机选取![]() 名大学生进行问卷调查,当被调查者问卷评分不低于
名大学生进行问卷调查,当被调查者问卷评分不低于![]() 分则认为其喜欢数学命题,当评分低于
分则认为其喜欢数学命题,当评分低于![]() 分则认为其不喜欢数学命题,问卷评分的茎叶图如下:
分则认为其不喜欢数学命题,问卷评分的茎叶图如下:
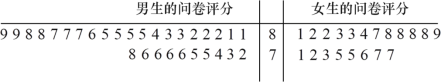
依据上述数据制成如下列联表:
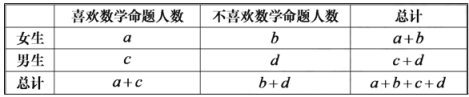
请问是否有![]() 的把握认为大学生是否喜欢数学命题与性别有关?
的把握认为大学生是否喜欢数学命题与性别有关?
参考公式及数据:![]() .
.
|
|
|
|
|
|
|
|
|
|
(2)在某次命题大赛中,![]() 同学要进行
同学要进行![]() 轮命题,其在每轮命题成功的概率均为
轮命题,其在每轮命题成功的概率均为![]() ,各轮命题相互独立,若该同学在
,各轮命题相互独立,若该同学在![]() 轮命题中恰有
轮命题中恰有![]() 次成功的概率为
次成功的概率为![]() ,记该同学在
,记该同学在![]() 轮命题中的成功次数为
轮命题中的成功次数为![]() ,求
,求![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了解某市的交通状况,现对其6条道路进行评估,得分分别为:5,6,7,8,9,10.规定评估的平均得分与全市的总体交通状况等级如表
评估的平均得分 | (0,6] | (6,8] | (8,10] |
全市的总体交通状况等级 | 不合格 | 合格 | 优秀 |
(1)求本次评估的平均得分,并参照上表估计该市的总体交通状况等级.
(2)用简单随机抽样方法从这6条道路中抽取2条,它们的得分组成一个样本,求该样本的平均数与总体的平均数之差的绝对值不超0.5的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】学校艺术节对同一类的![]() ,
,![]() ,
,![]() ,
,![]() 四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
甲说:“是![]() 或
或![]() 作品获得一等奖”;
作品获得一等奖”;
乙说:“![]() 作品获得一等奖”;
作品获得一等奖”;
丙说:“![]() ,
,![]() 两项作品未获得一等奖”;
两项作品未获得一等奖”;
丁说:“是![]() 作品获得一等奖”.
作品获得一等奖”.
若这四位同学中只有两位说的话是对的,则获得一等奖的作品是__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com