
科目: 来源: 题型:
【题目】已知椭圆![]() 的左焦点在抛物线
的左焦点在抛物线![]() 的准线上,且椭圆的短轴长为2,
的准线上,且椭圆的短轴长为2,![]() 分别为椭圆的左,右焦点,
分别为椭圆的左,右焦点,![]() 分别为椭圆的左,右顶点,设点
分别为椭圆的左,右顶点,设点![]() 在第一象限,且
在第一象限,且![]() 轴,连接
轴,连接![]() 交椭圆于点
交椭圆于点![]() ,直线
,直线![]() 的斜率为
的斜率为![]() .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)若三角形![]() 的面积等于四边形
的面积等于四边形![]() 的面积,求
的面积,求![]() 的值;
的值;
(Ⅲ)设点![]() 为
为![]() 的中点,射线
的中点,射线![]() (
(![]() 为原点)与椭圆交于点
为原点)与椭圆交于点![]() ,满足
,满足![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某高中志愿者男志愿者5人,女志愿者3人,这些人要参加社区服务工作.从这些人中随机抽取4人负责文明宣传工作,另外4人负责卫生服务工作.
(Ⅰ)设![]() 为事件;“负责文明宣传工作的志愿者中包含女志愿者甲但不包含男志愿者乙”,求事件
为事件;“负责文明宣传工作的志愿者中包含女志愿者甲但不包含男志愿者乙”,求事件![]() 发生的概率;
发生的概率;
(Ⅱ)设![]() 表示参加文明宣传工作的女志愿者人数,求随机变量
表示参加文明宣传工作的女志愿者人数,求随机变量![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 内,动点
内,动点![]() 到定点
到定点![]() 的距离与
的距离与![]() 到定直线
到定直线![]() 距离之比为
距离之比为![]() .
.
(Ⅰ)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)设点![]() 是轨迹
是轨迹![]() 上两个动点直线
上两个动点直线![]() 与轨迹
与轨迹![]() 的另一交点分别为
的另一交点分别为![]() 且直线
且直线![]() 的斜率之积等于
的斜率之积等于![]() ,问四边形
,问四边形![]() 的面积
的面积![]() 是否为定值?请说明理由.
是否为定值?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】由团中央学校部、全国学联秘书处、中国青年报社共同举办的2018年度全国“最美中学生“寻访活动结果出炉啦,此项活动于2018年6月启动,面向全国中学在校学生,通过投票方式寻访一批在热爱祖国、勤奋学习、热心助人、见义勇为等方面表现突出、自觉树立和践行社会主义核心价值观的“最美中学生”.现随机抽取了30名学生的票数,线成如图所示的茎叶图,若规定票数在65票以上(包括65票)定义为风华组.票数在65票以下(不包括65票)的学生定义为青春组.

(Ⅰ)在这30名学生中,青春组学生中有男生7人,风华组学生中有女生12人,试问有没有![]() 的把握认为票数分在青春组或风华组与性别有关;
的把握认为票数分在青春组或风华组与性别有关;
(Ⅱ)如果用分层抽样的方法从青春组和风华组中抽取5人,再从这5人中随机抽取2人,那么至少有1人在青春组的概率是多少?
(Ⅲ)用样本估计总体,把频率作为概率,若从该地区所有的中学(人数很多)中随机选取4人,用![]() 表示所选4人中青春组的人数,试写出
表示所选4人中青春组的人数,试写出![]() 的分布列,并求出
的分布列,并求出![]() 的数学期望.
的数学期望.
附: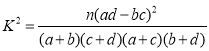 ;其中
;其中![]()
独立性检验临界表:
| 0.100 | 0.050 | 0.010 |
| 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目: 来源: 题型:
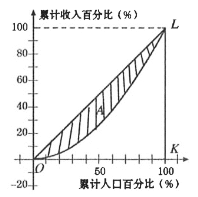
【题目】为了研究国民收入在国民之间的分配,避免贫富过分悬殊,美国统计学家劳伦茨提出了著名的劳伦茨曲线,如图所示:劳伦茨曲线为直线![]() 时,表示收入完全平等,劳伦茨曲线为折线
时,表示收入完全平等,劳伦茨曲线为折线![]() 时,表示收入完全不平等记区域
时,表示收入完全不平等记区域![]() 为不平等区域,
为不平等区域,![]() 表示其面积,
表示其面积,![]() 为
为![]() 的面积.将
的面积.将![]() ,称为基尼系数.对于下列说法:
,称为基尼系数.对于下列说法:
①![]() 越小,则国民分配越公平;
越小,则国民分配越公平;
②设劳伦茨曲线对应的函数为![]() ,则对
,则对![]() ,均有
,均有![]() ;
;
③若某国家某年的劳伦茨曲线近似为![]() ,则
,则![]() ;
;
④若某国家某年的劳伦茨曲线近似为![]() ,则
,则![]() .
.
其中不正确的是:( )
A.①④B.②③C.①③④D.①②④
查看答案和解析>>
科目: 来源: 题型:
【题目】在极坐标系![]() 中,曲线
中,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]() ,设
,设![]() 与
与![]() 交于
交于![]() 、
、![]() 两点,
两点,![]() 中点为
中点为![]() ,
,![]() 的垂直平分线交
的垂直平分线交![]() 于
于![]() 、
、![]() .以
.以![]() 为坐标原点,极轴为
为坐标原点,极轴为![]() 轴的正半轴建立直角坐标系
轴的正半轴建立直角坐标系![]() .
.
(1)求![]() 的直角坐标方程与点
的直角坐标方程与点![]() 的直角坐标;
的直角坐标;
(2)求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com