【题目】在直角坐标系中，直线的参数方程为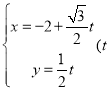为参数），以坐标原点为极点，轴的正半轴为极轴建立极坐标系，曲线的极坐标方程为.

（1）求曲线的直角坐标方程与直线的极坐标方程；

（2）若射线与曲线交于点（不同于原点），与直线交于点，直线与极轴所在直线交于点.求的值.

【题目】已知函数.

（1）当且时，求函数的单调区间；

（2）当时，若函数的两个极值点分别为、，证明.

【题目】已知过椭圆的左焦点，作斜率为的直线，交椭圆于两点.

（1）若原点到直线的距离为，求直线的方程；

（2）设点，直线与椭圆交于另一点，直线与椭圆交于另一点.设的斜率为，则是否为定值?若是，求出该定值；若不是，请说明理由.

（1）补充完整所给表格，并根据表格数据计算是否有的把握认为看春晚后会思考节目体现的文化内涵、历史背景等与文理科学生有关；

（2）①现从上表的”思考过”的文理科学生中按分层抽样选出7人.再从这7人中随机抽取4人，记这4人中“文科学生”的人数为,试求的分布列与数学期望；

②现设计一份试卷（题目知识点来自春晚相关知识整合与变化），假设“思考过”的学生及格率为，“没有思考过”的学生的及格率为.现从“思考过”与“没有思考过”的学生中分别随机抽取一名学生进行测试，求两人至少有一个及格的概率.

附参考公式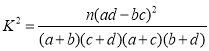：，其中.

参考数据：

【题目】如图，在四棱锥中，底面，底面是直角梯形，，.

（1）证明：当点在上运动时，始终有平面平面；

（2）求锐二而角的余弦值.

【题目】某地的中小学办学条件在政府的教育督导下，迅速得到改变.教育督导一年后.分别随机抽查了初中（用表示）与小学（用表示）各10所学校.得到相关指标的综合评价得分（百分制）的茎叶图如图所示.则从茎叶图可得出正确的信息为（ ）（80分及以上为优秀）. ①初中得分与小学得分的优秀率相同；②初中得分与小学得分的中位数相同③初中得分的方差比小学得分的方差大④初中得分与小学得分的平均分相同.

A.①②B.①③C.②④D.③④

【题目】已知函数 .

（1）当时，

①求曲线在点处的切线方程；

②求函数在区间上的值域.

（2）对于任意，都有，求实数的取值范围.

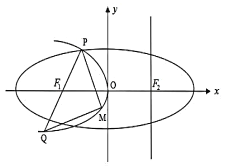
【题目】如图，设抛物线的准线与轴交于椭圆的右焦点为的左焦点.椭圆的离心率为，抛物线与椭圆交于轴上方一点，连接并延长其交于点， 为上一动点，且在之间移动.

（1）当取最小值时，求和的方程；

（2）若的边长恰好是三个连续的自然数，当面积取最大值时，求面积最大值以及此时直线的方程．

【题目】2018 年1月16日，由新华网和中国财经领袖联盟联合主办的2017中国财经年度人物评选结果揭晓，某知名网站财经频道为了解公众对这些年度人物是否了解，利用网络平台进行了调查，并从参与调查者中随机选出人，把这人分为 两类（类表示对这些年度人物比较了解，类表示对这些年度人物不太了解），并制成如下表格：

（1）若按照年龄段进行分层抽样，从这人中选出人进行访谈，并从这人中随机选出两名幸运者给予奖励.求其中一名幸运者的年龄在岁～岁之间，另一名幸运者的年龄在岁～岁之间的概率；(注：从人中随机选出人,共有种不同选法)

（2）如果把年龄在 岁～岁之间的人称为青少年，年龄在岁～岁之间的人称为中老年，则能否在犯错误的概率不超过的前提下认为青少年与中老年人在对财经年度人物的了解程度上有差异？

参考数据：

，其中