
科目: 来源: 题型:
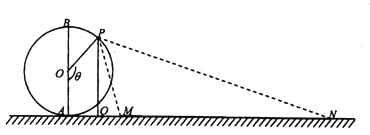
【题目】如图,摩天轮的半径![]() 为
为![]() ,它的最低点
,它的最低点![]() 距地面的高度忽略不计.地上有一长度为
距地面的高度忽略不计.地上有一长度为![]() 的景观带
的景观带![]() ,它与摩天轮在同一竖直平面内,且
,它与摩天轮在同一竖直平面内,且![]() .点
.点![]() 从最低点
从最低点![]() 处逆时针方向转动到最高点
处逆时针方向转动到最高点![]() 处,记
处,记![]() .
.
(1)当![]() 时,求点
时,求点![]() 距地面的高度
距地面的高度![]() ;
;
(2)试确定![]() 的值,使得
的值,使得![]() 取得最大值.
取得最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,将曲线
中,将曲线![]() :
:![]() 上的点按坐标变换
上的点按坐标变换![]() ,得到曲线
,得到曲线![]() ,
,![]() 为
为![]() 与
与![]() 轴负半轴的交点,经过点
轴负半轴的交点,经过点![]() 且倾斜角为
且倾斜角为![]() 的直线
的直线![]() 与曲线
与曲线![]() 的另一个交点为
的另一个交点为![]() ,与曲线
,与曲线![]() 的交点分别为
的交点分别为![]() ,
,![]() (点
(点![]() 在第二象限).
在第二象限).
(Ⅰ)写出曲线![]() 的普通方程及直线
的普通方程及直线![]() 的参数方程;
的参数方程;
(Ⅱ)求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】惰性气体分子为单原子分子,在自由原子情形下,其电子电荷分布是球对称的.负电荷中心与原子核重合,但如两个原子接近,则彼此能因静电作用产生极化(正负电荷中心不重合),从而导致有相互作用力,这称为范德瓦尔斯相互作用.今有两个相同的惰性气体原子,它们的原子核固定,原子核正电荷的电荷量为![]() ,这两个相距为
,这两个相距为![]() 的惰性气体原子组成体系的能量中有静电相互作用能
的惰性气体原子组成体系的能量中有静电相互作用能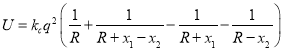 ,其中
,其中![]() 为静电常量,
为静电常量,![]() ,
,![]() 分别表示两个原子负电中心相对各自原子核的位移,且
分别表示两个原子负电中心相对各自原子核的位移,且![]() 和
和![]() 都远小于
都远小于![]() ,当
,当![]() 远小于1时,
远小于1时,![]() ,则
,则![]() 的近似值为( )
的近似值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】我们正处于一个大数据飞速发展的时代,对于大数据人才的需求也越来越大,其岗位大致可分为四类:数据开发、数据分析、数据挖掘、数据产品.某市2019年这几类工作岗位的薪资(单位:万元/月)情况如下表所示:
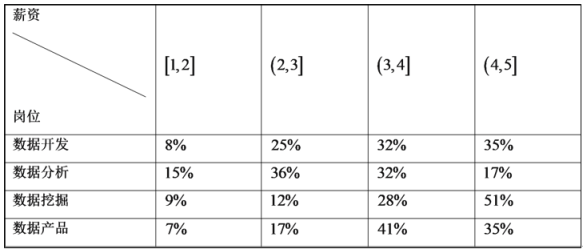
由表中数据可得该市各类岗位的薪资水平高低情况为( )
A.数据挖掘>数据开发>数据产品>数据分析
B.数据挖掘>数据产品>数据开发>数据分析
C.数据挖掘>数据开发>数据分析>数据产品
D.数据挖掘>数据产品>数据分析>数据开发
查看答案和解析>>
科目: 来源: 题型:
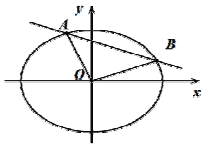
【题目】已知椭圆![]()
![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() ,直线
,直线![]() 交椭圆
交椭圆![]() 于不同的两点
于不同的两点![]() ,设线段
,设线段![]() 的中点为
的中点为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)当![]() 的面积为
的面积为![]() (其中
(其中![]() 为坐标原点)且
为坐标原点)且![]() 时,试问:在坐标平面上是否存在两个定点
时,试问:在坐标平面上是否存在两个定点![]() ,使得当直线
,使得当直线![]() 运动时,
运动时,![]() 为定值?若存在,求出点
为定值?若存在,求出点![]() 的坐标和定值;若不存在,请说明理由.
的坐标和定值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】2019年全国“两会”,即中华人民共和国第十三届全国人大二次会议和中国人民政治协商会议第十三届全国会第二次会议,分别于2019年3月5日和3月3日在北京召开.为了了解哪些人更关注“两会”,某机构随机抽取了年龄在![]() 岁之间的200人进行调查,并按年龄绘制出频率分布直方图,如图.
岁之间的200人进行调查,并按年龄绘制出频率分布直方图,如图.
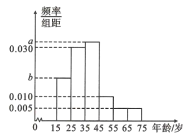
若把年龄在区间![]() ,
,![]() 内的人分别称为“青少年”“中老年”.经统计“青少年”和“中老年”的人数之比为
内的人分别称为“青少年”“中老年”.经统计“青少年”和“中老年”的人数之比为![]() .其中“青少年”中有40人关注“两会”,“中老年”中关注“两会”和不关注“两会”的人数之比为
.其中“青少年”中有40人关注“两会”,“中老年”中关注“两会”和不关注“两会”的人数之比为![]() .
.
(1)求图中![]() 的值.
的值.
(2)现采用分层抽样在![]() 和
和![]() 中随机抽取8人作为代表,从8人中任选2人,求2人都是“中老年”的概率.
中随机抽取8人作为代表,从8人中任选2人,求2人都是“中老年”的概率.
(3)根据已知条件,完成下面的![]() 列联表,并判断能否有
列联表,并判断能否有![]() %的把握认为“中老年”比“青少年”更加关注“两会”.
%的把握认为“中老年”比“青少年”更加关注“两会”.
关注 | 不关注 | 总计 | |
“青少年” | |||
“中老年” | |||
总计 |
附: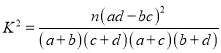 ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四面体ABCD中,O、E分别是BD、BC的中点,![]() ,
,![]() .
.
(1)求证:![]() 平面BCD;
平面BCD;
(2)求异面直线AB与CD所成角的余弦值;
(3)求点E到平面ACD的距离。

查看答案和解析>>
科目: 来源: 题型:
【题目】已知平面![]() 及直线
及直线![]() ,
,![]() ,则下列说法错误的个数是( ).
,则下列说法错误的个数是( ).
①若直线![]() ,
,![]() 与平面
与平面![]() 所成角都是
所成角都是![]() ,则这两条直线平行;②若直线
,则这两条直线平行;②若直线![]() ,
,![]() 与平面
与平面![]() 所成角都是
所成角都是![]() ,则这两条直线不可能垂直;③若直线
,则这两条直线不可能垂直;③若直线![]() ,
,![]() 垂直,则这两条直线与平面
垂直,则这两条直线与平面![]() 不可能都垂直;④若直线
不可能都垂直;④若直线![]() ,
,![]() 平行,则这两条直线中至少有一条与平面
平行,则这两条直线中至少有一条与平面![]() 平行.
平行.
A.1B.2C.3D.4
查看答案和解析>>
科目: 来源: 题型:
【题目】某生物兴趣小组对冬季昼夜温差与反季节新品种大豆发芽数之间的关系进行研究,他们分别记录了![]() 月
月![]() 日至11月25日每天的昼夜温差与实验室每天100颗种子的发芽数,得到以下表格
日至11月25日每天的昼夜温差与实验室每天100颗种子的发芽数,得到以下表格
日期 | 11月21日 | 11月22日 | 11月23日 | 11月24日 | 11月25日 |
温差( | 8 | 9 | 11 | 10 | 7 |
发芽数(颗) | 22 | 26 | 31 | 27 | 19 |
该兴趣小组确定的研究方案是:先从这5组数据中选取2组数据,然后用剩下的3组数据求线性回归方程,再用被选取的![]() 组数据进行检验.
组数据进行检验.
(1)求统计数据中发芽数的平均数与方差;
(2)若选取的是11月21日与11月25日的两组数据,请根据11月22 日至11月24 日的数据,求出发芽数![]() 关于温差
关于温差![]() 的线性回归方程
的线性回归方程![]() ,若由线性回归方程得到的估计数据与所选取的检验数据的误差不超过2,则认为得到的线性回归方程是可靠的,问得到的线性回归方程是否可靠?
,若由线性回归方程得到的估计数据与所选取的检验数据的误差不超过2,则认为得到的线性回归方程是可靠的,问得到的线性回归方程是否可靠?
附:线性回归方程 中斜率和截距最小二乘估法计算公式: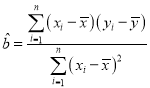 ,
,![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com