
 圆弧,AC的竖直高度差h=0.45m.在紧靠管道出口D处有一水平放置且绕其水平中心轴OO′匀速旋转的圆筒,圆筒直径d=0.15m,圆筒上开有小孔E.现有质量为m=0.1kg且可视为质点的小球由静止开始从管口A滑下,小球滑到管道出口D处时,恰好能从小孔E竖直进入圆筒,随后,小球由小孔E处竖直向上穿出圆筒.不计空气阻力,取g=10m/s2.求:
圆弧,AC的竖直高度差h=0.45m.在紧靠管道出口D处有一水平放置且绕其水平中心轴OO′匀速旋转的圆筒,圆筒直径d=0.15m,圆筒上开有小孔E.现有质量为m=0.1kg且可视为质点的小球由静止开始从管口A滑下,小球滑到管道出口D处时,恰好能从小孔E竖直进入圆筒,随后,小球由小孔E处竖直向上穿出圆筒.不计空气阻力,取g=10m/s2.求:
 (2n+1)(n=0,1,2,3…),要求周期T,则必须求出小球上抛的时间t,已知位移d,须知小球的速度vD,那么就要分析小球由A到D的过程由机械能守恒定律求出vD.
(2n+1)(n=0,1,2,3…),要求周期T,则必须求出小球上抛的时间t,已知位移d,须知小球的速度vD,那么就要分析小球由A到D的过程由机械能守恒定律求出vD.

 )=m(g+
)=m(g+ )
) )N=4.6N
)N=4.6N  m
m
 =
= m/s=2m/s
m/s=2m/s  gt2
gt2 (2n+1)(n=0,1,2,3…),
(2n+1)(n=0,1,2,3…), =
= s (n=0,1,2,3…).
s (n=0,1,2,3…). =
= s (n=0,1,2,3…).
s (n=0,1,2,3…).

 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中物理 来源: 题型:
 如图所示,内壁光滑的圆台形容器固定不动,其轴线沿竖直方向.使一小球先后在M和N两处紧贴着容器内壁分别在图中虚线所示的水平面内做匀速圆周运动,则小球( )
如图所示,内壁光滑的圆台形容器固定不动,其轴线沿竖直方向.使一小球先后在M和N两处紧贴着容器内壁分别在图中虚线所示的水平面内做匀速圆周运动,则小球( )查看答案和解析>>
科目:高中物理 来源: 题型:
 (2011?河东区一模)如图所示,内壁光滑的木槽质量为mA=m,内直径为2L,置于水平桌面上,槽与桌面间的动摩擦因数为μ.槽内有两个小球B、C,它们的质量分别是mB=m,mC=2m.现用两球将很短的轻弹簧压紧(球与弹簧不连接),且B球到木槽左端、C球到木槽右端的距离均为L,这时弹簧的弹性势能为EP=μmgL.同时释放B、C球,并假设小球与槽碰撞后不分离,碰撞时间不计.求:
(2011?河东区一模)如图所示,内壁光滑的木槽质量为mA=m,内直径为2L,置于水平桌面上,槽与桌面间的动摩擦因数为μ.槽内有两个小球B、C,它们的质量分别是mB=m,mC=2m.现用两球将很短的轻弹簧压紧(球与弹簧不连接),且B球到木槽左端、C球到木槽右端的距离均为L,这时弹簧的弹性势能为EP=μmgL.同时释放B、C球,并假设小球与槽碰撞后不分离,碰撞时间不计.求:查看答案和解析>>
科目:高中物理 来源: 题型:
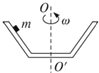 如图所示,内壁光滑的装置绕竖直轴匀速旋转,有一紧贴内壁的小物体,物体随装置一起在水平面内匀速转动的过程中所受外力可能是( )
如图所示,内壁光滑的装置绕竖直轴匀速旋转,有一紧贴内壁的小物体,物体随装置一起在水平面内匀速转动的过程中所受外力可能是( )| A、下滑力、弹力、静摩擦力 | B、重力、弹力、滑动摩擦力 | C、重力、弹力 | D、重力、弹力、向心力 |
查看答案和解析>>
科目:高中物理 来源: 题型:
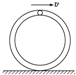 如图所示,内壁光滑的导管弯成圆周轨道竖直放置,其质量为2m,小球质量为m,在管内滚动,当小球运动到最高点时,导管刚好要离开地面.(轨道半径为R)求:
如图所示,内壁光滑的导管弯成圆周轨道竖直放置,其质量为2m,小球质量为m,在管内滚动,当小球运动到最高点时,导管刚好要离开地面.(轨道半径为R)求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com