
 如图所示,在MN下方存在竖立向上的匀强电场,Ⅰ、Ⅱ区域存在方向相反的匀强磁场,已知Ⅰ区域的磁感应强度大小为B1,方向垂直纸面向里,PQ为绝缘薄板且为两磁场的理想边界,C、D为板上两个小孔,AO为CD的中垂线,交点为A,O为I磁场区域的上边界MN与AO的交点.质量为m、电量为q的带电小球从O点正上方高为h的某点由静止开始下落,进入Ⅰ区域后,恰能做匀速圆周运动,已知重力加速度为g.
如图所示,在MN下方存在竖立向上的匀强电场,Ⅰ、Ⅱ区域存在方向相反的匀强磁场,已知Ⅰ区域的磁感应强度大小为B1,方向垂直纸面向里,PQ为绝缘薄板且为两磁场的理想边界,C、D为板上两个小孔,AO为CD的中垂线,交点为A,O为I磁场区域的上边界MN与AO的交点.质量为m、电量为q的带电小球从O点正上方高为h的某点由静止开始下落,进入Ⅰ区域后,恰能做匀速圆周运动,已知重力加速度为g.分析 (1)带电小球进入复合场后,做匀速圆周运动,知电场力和重力平衡,洛伦兹力提供向心力,根据平衡得出粒子的电性以及求出电场强度的大小.
(2)根据机械能守恒定律求出粒子进入磁场前的速度,结合半径公式和几何关系求出Ⅰ区域的磁场宽度d和C、A间的距离L;
(3)作出粒子的运动轨迹图,结合周期公式,以及几何关系求出带电小球自O点进入磁场到第一次回到O点所用的时间.
解答 解:(1)带电小球进入复合场后,恰能做匀速圆周运动,合力为洛伦兹力,重力与电场力平衡,重力竖直向下,电场力竖直向上,即小球带正电.
由qE=mg,
解得:E=$\frac{mg}{q}$.
(2)带电小球在进入磁场前做自由落体运动,由机械能守恒得:$mgh=\frac{1}{2}m{v}^{2}$,
带电小球在Ⅰ区域内做匀速圆周运动,洛伦兹力提供向心力,有:$qv{B}_{1}=m\frac{{v}^{2}}{{R}_{1}}$,
由几何关系得:d=R1sin60°,L=R1(1-cos60°),
解得:d=$\frac{m\sqrt{6gh}}{2q{B}_{1}}$,L=$\frac{{R}_{1}}{2}=\frac{m\sqrt{2gh}}{2q{B}_{1}}$.
(3)带电小球在Ⅱ区域内做匀速圆周运动,有:$qv{B}_{2}=m\frac{{v}^{2}}{{R}_{2}}$,
由几何关系得,R2=2L=R1,
解得:B2=B1,
带电小球在Ⅰ、Ⅱ区域内的运动周期为:${T}_{1}={T}_{2}=\frac{2π{R}_{2}}{v}$,
带电小球在Ⅰ、Ⅱ区域内的运动的总时间为:t=$2×\frac{{T}_{1}}{6}+\frac{5}{6}{T}_{2}=\frac{7}{6}{T}_{2}$.
解得:t=$\frac{7πm}{3q{B}_{1}}$.
答:(1)小球带正电,电场强度为$\frac{mg}{q}$.
(2)Ⅰ区域的磁场宽度为$\frac{m\sqrt{6gh}}{2q{B}_{1}}$,C、A间的距离为$\frac{m\sqrt{2gh}}{2q{B}_{1}}$.
(3)Ⅱ区域的磁感应强度B2的大小为B1,带电小球自O点进入磁场到第一次回到O点所用的时间为$\frac{7πm}{3q{B}_{1}}$.
点评 本题考查了带电小球在磁场中的运动,分析清楚小球的运动过程,作出小球的运动轨迹、应用机械能守恒定律、牛顿第二定律、功的计算公式即可正确解题;分析清楚运动过程、作出小球运动轨迹是正确解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中物理 来源: 题型:多选题
| A. | 火星和地球的质量之比 | |
| B. | 火星和地球到太阳的距离之比 | |
| C. | 火星和太阳的质量之比 | |
| D. | 火星和地球绕太阳运行速度大小之比 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题

查看答案和解析>>
科目:高中物理 来源: 题型:解答题

查看答案和解析>>
科目:高中物理 来源: 题型:解答题
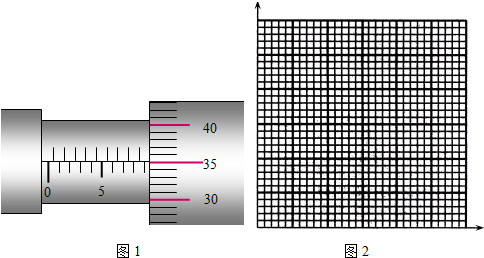
| 次数 | 1 | 2 | 3 | 4 | 5 | 6 |
| 距离x/m | 0.10 | 0.20 | 0.30 | 0.40 | 0.50 | 0.60 |
| 速度v/ms-1 | 1.00 | 1.42 | 1.73 | 2.01 | 2.32 | 2.44 |
| 速度的平方v2/(m•s-1)2 | 1.00 | 2.02 | 2.99 | 4.04 | 5.38 | 5.95 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 根据波尔原子结构理论,氦离子(He+)的能级图如图所示,当某个He+处在n=4的激发态时,由于跃迁所发射的谱线可能有几条( )
根据波尔原子结构理论,氦离子(He+)的能级图如图所示,当某个He+处在n=4的激发态时,由于跃迁所发射的谱线可能有几条( )| A. | 1条 | B. | 2条 | C. | 3条 | D. | 6条 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
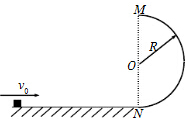 如图,质量m=1.0kg的物体(可视为质点)以v0=10m/s的初速度从水平面的某点向右运动并冲上半径R=1.0m的竖直光滑半圆环,物体与水平面间的动摩擦因数μ=0.5.求:
如图,质量m=1.0kg的物体(可视为质点)以v0=10m/s的初速度从水平面的某点向右运动并冲上半径R=1.0m的竖直光滑半圆环,物体与水平面间的动摩擦因数μ=0.5.求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 月球绕O点转动的角速度减小 | B. | 月球绕O点转动的角速度增大 | ||
| C. | 地球球心到O点的距离减小 | D. | 月球绕O点转动的动能增加 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com