
 如图所示,在区域I和区域Ⅱ内分别存在匀强电场,电场强度大小均为E,但方向不同.在区域I内场强方向沿y轴正方向,区域Ⅱ内场强方向未标明,两处电场都处在xoy平面内.一质量为m,电量为q的正粒子从坐标原点O以某一初速度沿x轴正方向射入电场区域I,从P点进入电场区域Ⅱ,到达Ⅱ区域右边界Q处时速度恰好为零.P点的坐标为(L,$\frac{L}{2}$).不计粒子所受重力,求:
如图所示,在区域I和区域Ⅱ内分别存在匀强电场,电场强度大小均为E,但方向不同.在区域I内场强方向沿y轴正方向,区域Ⅱ内场强方向未标明,两处电场都处在xoy平面内.一质量为m,电量为q的正粒子从坐标原点O以某一初速度沿x轴正方向射入电场区域I,从P点进入电场区域Ⅱ,到达Ⅱ区域右边界Q处时速度恰好为零.P点的坐标为(L,$\frac{L}{2}$).不计粒子所受重力,求:分析 看似复杂的题目,仔细分析实际上是两种基本运动的组合:类平抛运动和匀减速直线运动,由运动学公式和牛顿第二定律不难求出.
(1)粒子在Ⅰ区内做类平抛运动,由于已知P点的坐标,则类平抛运动的水平位移和竖直位移为已知,而电场强度已知,则加速度为已知.则由运动学公式和牛顿第二定律就能求出类平抛的初速度.
(2)进入Ⅱ区后,由于到达P点的速度为零,则从P到Q粒子是做匀减速直线运动,它的初速度就是类平抛的末速度vp,而加速度已知,则由匀减速直线运动位移与速度的关系就能求出位移,从而求出Ⅱ区的宽度.
解答 解:(1)设带电粒子射入电场区域Ⅰ时的初速度为v0
在x轴正方向,粒子做匀速直线运动:L=v0t ①
在y轴正方向,粒子做初速度为零的匀加速直线运动:$\frac{L}{2}=\frac{1}{2}a{t}^{2}$ ②
由牛顿第二定律:$a=\frac{qE}{m}$
解得:${v}_{0}=\sqrt{\frac{qEL}{m}}$
(2)粒子在区域Ⅱ做匀减速直线运动,设粒子在P处的速度vp,x方向的分速度为vpx
在y轴方向的分速度为vpy,电场区域Ⅱ的宽度为△x2,则:
${v}_{px}={v}_{0}=\sqrt{\frac{qEL}{m}}$
${{v}_{py}}^{2}=\sqrt{{{v}_{px}}^{2}+{{v}_{py}}^{2}}$ 即 ${v}_{py}=\sqrt{\frac{qEL}{m}}$
故 ${v}_{p}=\sqrt{{{v}_{px}}^{2}+{{v}_{py}}^{2}}$=$\sqrt{\frac{2qEL}{m}}$
因为:$tgθ=\frac{{v}_{py}}{vpx}$ 所以:$θ=\frac{π}{4}$
设粒子从P做直线运动到Q所通过的位移为S,则有:
$0-{{v}_{p}}^{2}=-2\frac{qEL}{m}S$
解得:S=L
△x2=Scos45°
解得:△${x}_{2}=\frac{\sqrt{2}}{2}L$
答:(1)带电粒子射入电场区域I时的初速度为$\sqrt{\frac{qEL}{m}}$.
(2)电场区域Ⅱ的宽度为$\frac{\sqrt{2}}{2}L$.
点评 本题的怪点在于粒子在Ⅱ区内只说明是以一定的初速度进入匀强电场Ⅱ后,粒子到达Q点的速度为零.若是做曲线运动,则只能有最小的速度但不会为零,所以只能是在做匀减速直线运动到速度为零,这样问题就简单了.


科目:高中物理 来源: 题型:多选题
| A. | 电路中的电流为0.6A | B. | 电阻R2的阻值为10Ω | ||
| C. | 三只电阻两端的总电压为21V | D. | 电阻R2的阻值为20Ω |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
 如图所示是示波器的部分构造示意图,真空室中阴极K不断发出初速度可忽略的电子,电子经电压U 0=1.82×l0 4V的电场加速后,由孔N沿长L=0.10m相距为d=0.02m的两平行金属板A、B间的中心轴线进入两板间,电子穿过A、B板后最终可打在中心为O的荧光屏CD上,光屏CD距A、B板右侧距离s=0.45m.若在A、B间加U AB=54.6V的电压.已知电子电荷最e=1.6×10 -19C,质量m=9.1×10 -31kg.
如图所示是示波器的部分构造示意图,真空室中阴极K不断发出初速度可忽略的电子,电子经电压U 0=1.82×l0 4V的电场加速后,由孔N沿长L=0.10m相距为d=0.02m的两平行金属板A、B间的中心轴线进入两板间,电子穿过A、B板后最终可打在中心为O的荧光屏CD上,光屏CD距A、B板右侧距离s=0.45m.若在A、B间加U AB=54.6V的电压.已知电子电荷最e=1.6×10 -19C,质量m=9.1×10 -31kg.查看答案和解析>>
科目:高中物理 来源: 题型:计算题
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
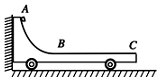 如图所示,水平光滑地面上停放着一辆质量为M=2kg的小车,小车左端靠在竖直墙壁上,其左侧半径为R=5m的四分之一圆弧轨道AB是光滑的,轨道最低点B与水平轨道BC相切相连,水平轨道BC长为3m,物块与水平轨道BC间的摩擦因素μ=0.4,整个轨道处于同一竖直平面内.现将质量为m=1kg的物块(可视为质点)从A点无初速度释放,取重力加速度为g=10m/s2.求:
如图所示,水平光滑地面上停放着一辆质量为M=2kg的小车,小车左端靠在竖直墙壁上,其左侧半径为R=5m的四分之一圆弧轨道AB是光滑的,轨道最低点B与水平轨道BC相切相连,水平轨道BC长为3m,物块与水平轨道BC间的摩擦因素μ=0.4,整个轨道处于同一竖直平面内.现将质量为m=1kg的物块(可视为质点)从A点无初速度释放,取重力加速度为g=10m/s2.求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
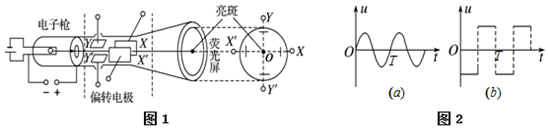
| A. | 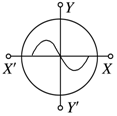 | B. | 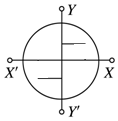 | C. |  | D. |  |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 欧姆定律适用于金属导电 | B. | 欧姆定律适用于电解质溶液导电 | ||
| C. | 欧姆定律适用于纯电阻电路导电 | D. | 欧姆定律适用于任何电路导电 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
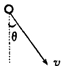 在匀强电场中,将质量为m,带电量为q的小球由静止释放,带电小球的运动轨迹为一直线,该直线与竖直方向的夹角为θ,如图所示,则电场强度的大小为( )
在匀强电场中,将质量为m,带电量为q的小球由静止释放,带电小球的运动轨迹为一直线,该直线与竖直方向的夹角为θ,如图所示,则电场强度的大小为( )| A. | 有唯一值$\frac{mgtanθ}{q}$ | B. | 最小值是$\frac{mgsinθ}{q}$ | C. | 最大值$\frac{mgtanθ}{q}$ | D. | $\frac{mg}{q}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com