
 ��ͼ��ʾ����y�������һ���Ϊ3d��ƽ�а�������������������PO��x���غϣ��ϰ�A�����磮һ����Ϊm�������Ϊq�����ӴӰ��P�����ٶ�v0���룬��y���Q��������ٶȷ�����y���ϸ�����ļнǦ�=30�㣻��y���Ҳ���һ��Բ����ǿ�ų�����Ÿ�Ӧǿ�ȵĴ�СB=$\frac{m{v}_{0}}{qd}$������ֱֽ��������Ӿ����ôų�������ܴ�O����x�Ḻ����ص��糡����֪OQ=d������������������
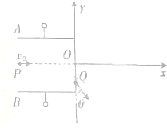
��ͼ��ʾ����y�������һ���Ϊ3d��ƽ�а�������������������PO��x���غϣ��ϰ�A�����磮һ����Ϊm�������Ϊq�����ӴӰ��P�����ٶ�v0���룬��y���Q��������ٶȷ�����y���ϸ�����ļнǦ�=30�㣻��y���Ҳ���һ��Բ����ǿ�ų�����Ÿ�Ӧǿ�ȵĴ�СB=$\frac{m{v}_{0}}{qd}$������ֱֽ��������Ӿ����ôų�������ܴ�O����x�Ḻ����ص��糡����֪OQ=d���������������������� ��1�������ٶȵĺϳɣ��������ӷɳ�����ʱ���ٶ�v�ķ������������֮��ĵ��Ʋ
��2�����ӽ���ų��������������ṩ������������Բ���˶������⣬ǡ����x�Ḻ����ص��糡��x�Ḻ����ص��糡�������켣���ɼ���֪ʶ����켣�뾶����С�����
��3�����ֱ���˶���ƽ���˶��� Բ���˶���ʱ���ϵ���ֱ�������ӵĸ��ε��˶���ʱ�䣬Ȼ����ͼ��ɣ�
��� �⣺��1�������ӷɳ���ʱˮƽ�ٶ�Ϊvx����ֱ�ٶ�Ϊvy��ˮƽƫת��Ϊ�ȣ���
ˮƽ����vx=v0 l=v0t1
��ֱ����vy=at1=$\frac{qEl}{m{v}_{0}}$=$\frac{qUl}{m{•3d•v}_{0}}$
��tan��=$\frac{{v}_{y}}{{v}_{0}}$=$tan60��=\sqrt{3}$��
����$\frac{qUl}{m•3d•{v}_{0}^{2}}$=$\sqrt{3}$����
ƫת����$d=\frac{1}{2}a{t}_{1}^{2}=\frac{1}{2}•\frac{qU}{m•3d}•\frac{{l}^{2}}{{v}_{0}^{2}}$����
�����٢ڵã�$l=\frac{2\sqrt{3}}{3}d$��$U=\frac{9m{v}_{0}^{2}}{2q}$��${t}_{1}=\frac{l}{{v}_{0}}=\frac{2\sqrt{3}d}{3{v}_{0}}$
��2����y���Q��������ٶȷ�����y���ϸ�����ļнǦ�=60�㣬�����ʱ���ٶȣ�
$v=\frac{{v}_{0}}{cos60��}=2{v}_{0}$
�������ڴų����˶��İ뾶ΪR�������������ṩ�����������qvB=m $\frac{{v}^{2}}{r}$
��$r=\frac{mv}{qB}=\frac{m•2{v}_{0}}{q•\frac{m{v}_{0}}{qd}}=2d$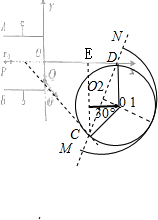
��ͼ��֪��O1C���ٶ�v�ķ���ֱ��$��C{O}_{1}D=��D{O}_{1}C=\frac{1}{2}��=30��$
������С�Ĵų��İ�Բ�İ뾶��$R=r+rsin30��=\frac{3}{2}r=3d$
�ų�����С�����${S}_{min}=\frac{1}{2}��{R}^{2}=\frac{9}{2}��{d}^{2}$
��3��������QC֮��������ֱ���˶����ڴų���������Բ���˶�����DO֮��������ֱ���˶�����ͼ��֪��
$CE=r+r•cos60��=\frac{3}{2}r=3d$��
��$QC=\frac{CE-OQ}{sin60��}=\frac{4d}{\sqrt{3}}$
$OE=QC•sin30��=\frac{2d}{\sqrt{3}}$=$\frac{2\sqrt{3}d}{3}$��$DE=r•sin60��=\sqrt{3}d$��$OD=OE+ED=\frac{5\sqrt{3}}{3}d$
�ã�${t}_{2}=\frac{QC}{{v}_{0}}=\frac{4\sqrt{3}d}{3{v}_{0}}$��${t}_{4}=\frac{DO}{{v}_{0}}=\frac{5\sqrt{3}d}{3{v}_{0}}$
��ͼ��֪�������ڴų��е�ƫת����240�㣬�����У�${t}_{3}=\frac{240��}{360��}T=\frac{2}{3}•\frac{2��r}{{v}_{0}}=\frac{8��d}{3{v}_{0}}$
�˶�����ʱ��Ϊ��t=t1+t2+t3+t4=$\frac{2\sqrt{3}d}{3{v}_{0}}+\frac{4\sqrt{3}d}{3{v}_{0}}+\frac{5\sqrt{3}d}{3{v}_{0}}+\frac{8��d}{3{v}_{0}}$=$\frac{��11\sqrt{3}+8�У�d}{3{v}_{0}}$
�𣺣�1���������ĵ��Ʋ���$\frac{9m{v}_{0}^{2}}{2q}$��
��2���ų��������С�����$\frac{9}{2}��{d}^{2}$��
��3�����Ӵӿ�ʼ�˶����ֻص��糡����ʱ����$\frac{��11\sqrt{3}+8�У�d}{3{v}_{0}}$��
���� �����д�����������ϳ����˶���Ҫ������ƽ���˶����о��������˶��ĺϳɺͷֽ⣬�ų��л��켣�ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | һ�����������ٶȷ���ֱ | |
| B�� | һ�����������ٶȷ�����ͬ | |
| C�� | һ�����������ٶȷ����෴ | |
| D�� | һ�����������ٶȷ�����ͬһ��ֱ���� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ���ǵĹ���뾶Խ�����������ٶ�ԽС | |
| B�� | ���ǵĹ���뾶Խ�����������ٶ�Խ�� | |
| C�� | ���ǵĹ���뾶Խ�����Ľ��ٶ�Խ�� | |
| D�� | ���ǵ�����һ��ʱ������뾶Խ������Ҫ��������Խ�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | б�۹��ĩ�����߱���ˮƽ | B�� | һ��Ҫ�ø��� | ||
| C�� | ÿ�ζ�Ҫƽ��С������Ħ���� | D�� | С��ÿ�ζ�Ӧ��б��ͬһ�߶��ͷ� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 ��ͼ��ʾ���ڿ��ȷֱ�Ϊa��b�����������ڷֱ������ǿ�Ȳ�ͬ�������෴����ǿ�ų����������ش�ֱ�����߽��ߵķ����M������ų������������ų���������ش�ֱ���Ҳ�߽��ߴ�N������������������ƣ������ӵ����������ֱ�e��m����������ų�ʱ���ٶ�ΪV����M��N������ƽ���ڴų��߽�ķ����ϵľ���ǡΪy=$\frac{a+b}{\sqrt{3}}$�������������ڴų��ĴŸ�Ӧǿ�ȷֱ�Ϊ���
��ͼ��ʾ���ڿ��ȷֱ�Ϊa��b�����������ڷֱ������ǿ�Ȳ�ͬ�������෴����ǿ�ų����������ش�ֱ�����߽��ߵķ����M������ų������������ų���������ش�ֱ���Ҳ�߽��ߴ�N������������������ƣ������ӵ����������ֱ�e��m����������ų�ʱ���ٶ�ΪV����M��N������ƽ���ڴų��߽�ķ����ϵľ���ǡΪy=$\frac{a+b}{\sqrt{3}}$�������������ڴų��ĴŸ�Ӧǿ�ȷֱ�Ϊ����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
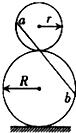 ��ͼ��ʾ���뾶�ֱ�Ϊr��R��Բ����ֱ���ţ����У���ˮƽ���ϣ�һ������б�ҹ���Բ�е��ҷֱ�����Բ�ཻ��a��b���㣮�ڴ�������һ���⻬�������һС���a���ɾ�ֹ�ͷţ���С���е�ʱ�����赲�����С���a���˶���b�����õ�ʱ�䣮
��ͼ��ʾ���뾶�ֱ�Ϊr��R��Բ����ֱ���ţ����У���ˮƽ���ϣ�һ������б�ҹ���Բ�е��ҷֱ�����Բ�ཻ��a��b���㣮�ڴ�������һ���⻬�������һС���a���ɾ�ֹ�ͷţ���С���е�ʱ�����赲�����С���a���˶���b�����õ�ʱ�䣮�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 ��ͼ��ʾ���ʵ���ǰ6s��ͨ����·����0.06m����6��8s�ڵ�ƽ���ٶȴ�СΪ0.02m/s������Ϊ�����������
��ͼ��ʾ���ʵ���ǰ6s��ͨ����·����0.06m����6��8s�ڵ�ƽ���ٶȴ�СΪ0.02m/s������Ϊ������������鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | 5.0V | B�� | 4.0V | C�� | 3.0V | D�� | ���ϴ𰸾��� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | �����ˣ�Ҫʹ���ָ�ȷ��Ӧ���Ӱڳ� | |
| B�� | �����ˣ�Ҫʹ���ָ�ȷ��Ӧ���̰ڳ� | |
| C�� | ����ˣ�Ҫʹ���ָ�ȷ��Ӧ���Ӱڳ� | |
| D�� | ����ˣ�Ҫʹ���ָ�ȷ��Ӧ���̰ڳ� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com